Contents
球面上の三角形の面積
理屈は考えず、公式集の結果だけを使います。 http://hooktail.sub.jp/vectoranalysis/SphereTriangle/ などを参考にしました。 原点をOとし、半径1の球面上の点A、B、Cがあり、∠AOBをc、∠AOCをb、∠BOCをaとします。 球面上の∠BAC(内角)をαとし、平面AOBと平面AOCの為す角とします。 平面AOBの平面AOCの為す角は平面AOBと平面AOCの法線の為す角とします。 平面AOCの単位法線はOAとOCの外積の規格化したものとします。
figure('color',[1,1,1],'position',[50,50,200,100]); st='$$\frac{\vec{OA}\times\vec{OC}}{|\vec{OA}\times\vec{OC}|}$$'; text(0,0.5,st,'interpreter','latex','Fontsize',18); axis off;
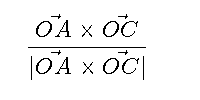
平面AOBの単位法線はOAとOBの外積を規格化したものとします。
figure('color',[1,1,1],'position',[50,50,200,100]); st='$$\frac{\vec{OA}\times\vec{OB}}{|\vec{OA}\times\vec{OB}|}$$'; text(0,0.5,st,'interpreter','latex','Fontsize',18); axis off;
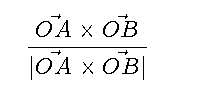
内角BACは平面AOCと平面AOBの法線の為す角ということで内積を用います。 外積と内積の公式を使ってカッコを展開します。
close all; figure('color',[1,1,1],'position',[50,50,650,200]); st1='$$\cos\alpha=\frac{\vec{OA}\times\vec{OC}}{|\vec{OA}\times\vec{OC}|}\cdot\frac{\vec{OA}\times\vec{OB}}{|\vec{OA}\times\vec{OB}|}$$'; st2='$$=\frac{(\vec{OA}\cdot\vec{OA})(\vec{OC}\cdot\vec{OB})-(\vec{OC}\cdot\vec{OA})(\vec{OA}\cdot\vec{OB})}{|\vec{OA}\times\vec{OC}||\vec{OA}\times\vec{OB}|}$$'; text(-0.1,0.75,st1,'interpreter','latex','Fontsize',18); text(0.02,0.25,st2,'interpreter','latex','Fontsize',18); axis off;
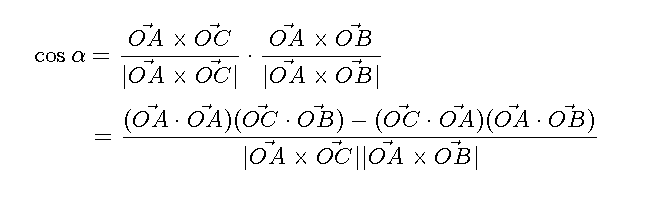
半径は1なので外積はsinだけとなり、絶対値のところは以下のようにかけます。
figure('color',[1,1,1],'position',[50,50,350,150]); st1='$$|\vec{OA}\times\vec{OC}|=\sin b$$'; st2='$$|\vec{OA}\times\vec{OB}|=\sin c$$'; st3='$$|\vec{OB}\times\vec{OC}|=\sin a$$'; text(0,0.8,st1,'interpreter','latex','Fontsize',18); text(0,0.5,st2,'interpreter','latex','Fontsize',18); text(0,0.2,st3,'interpreter','latex','Fontsize',18); axis off;
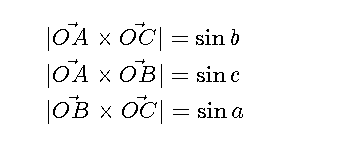
内積・外積をcos、sinで書き換えます。
figure('color',[1,1,1],'position',[50,50,350,100]); st='$$\cos\alpha=\frac{\cos a -\cos b \cos c}{\sin b \sin c}$$'; text(0,0.5,st,'interpreter','latex','Fontsize',18); axis off;
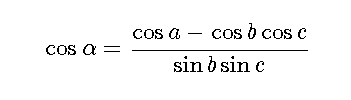
球面上の三角形の面積Sは、内角をα、β、γ、半径をRとすると以下の公式が使えます。
figure('color',[1,1,1],'position',[50,50,350,100]); st='$$S=R^2(\alpha+\beta+\gamma-\pi)$$'; text(0,0.5,st,'interpreter','latex','Fontsize',18); axis off;
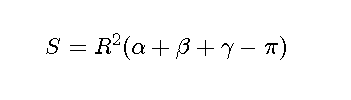
半径1のときの球面上の3点ABCが為す三角形の面積は以下の通りになります。
close all; figure('color',[1,1,1],'position',[50,50,1000,200]); st1='$$S=\cos^{-1}\alpha+\cos^{-1}\beta+\cos^{-1}\gamma-\pi$$'; st2='$$=\cos^{-1}\frac{\cos a - \cos b \cos c}{\sin b \sin c}+\cos^{-1}\frac{\cos b - \cos c \cos a}{\sin c \sin a}+\cos^{-1}\frac{\cos c - \cos b \cos a}{\sin a \sin b}-\pi$$'; text(-0.1,0.75,st1,'interpreter','latex','Fontsize',18); text(-0.07,0.25,st2,'interpreter','latex','Fontsize',18); axis off;
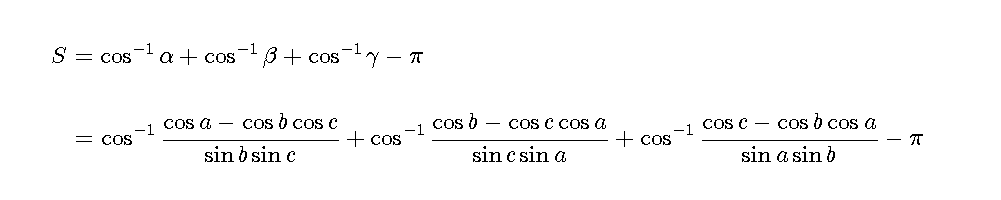
メッシュの内外判定
ある点が三角メッシュの内か外かの判定は、その点を中心とした各三角メッシュの立体角の総和が±4π,±12π,±20π・・・かどうかとなります。 MATLABにあるmriファイルで試してみます。 isosurface関数を使ってメッシュを作成しますが、そのままだとメッシュが閉じてくれないので、蓋を作るべく、上下にゼロ行列を挿入します。
clear;close all; load mri; D=squeeze(D); D0=repmat(uint8(0),[siz(1),siz(2),1]); D=cat(3,D0,D,D0); hmesh=isosurface(D,1); hmesh=reducepatch(hmesh,5000); hmesh.vertices(:,3)=hmesh.vertices(:,3)*2.5; figure('color',[1,1,1]); hskull=patch(hmesh,'edgecolor','none','facecolor',[1,0.5,0.5]); set(hskull,'facealpha',0.1);hold on; daspect([1,1,1]); axis off;axis tight; rotate3d on;view([40,25]);

1cmおきに格子点を設け、メッシュの内外判定を行い、メッシュの内側だけ表示させます。
sg=10; limx=round(xlim/sg)*sg; limy=round(ylim/sg)*sg; limz=round(zlim/sg)*sg; limx=min(limx):sg:max(limx); limy=min(limy):sg:max(limy); limz=min(limz):sg:max(limz); [x,y,z]=meshgrid(limx,limy,limz); P=[x(:),y(:),z(:)]; S=zeros(size(P,1),1); N=size(P,1); pt=1:N; nv=size(hmesh.vertices,1); for n=1:N p=hmesh.vertices-ones(nv,1)*P(n,:); p=p./(sum(p.^2,2).^0.5*ones(1,3)); p1=p(hmesh.faces(:,1),:); p2=p(hmesh.faces(:,2),:); p3=p(hmesh.faces(:,3),:); ang1=acos(sum(p1.*p2,2)); ang2=acos(sum(p2.*p3,2)); ang3=acos(sum(p3.*p1,2)); ca1=cos(ang1);sa1=sin(ang1); ca2=cos(ang2);sa2=sin(ang2); ca3=cos(ang3);sa3=sin(ang3); s=acos((ca1-ca2.*ca3)./(sa2.*sa3))+acos((ca2-ca3.*ca1)./(sa3.*sa1))+acos((ca3-ca2.*ca1)./(sa1.*sa2))-pi; s=sum(s)/pi; S(n)=s; if s<3.95 pt(n)=0; end; end; pt(pt==0)=[]; plot3(P(pt,1),P(pt,2),P(pt,3),'b.'); daspect([1,1,1]);view([40,25]); rotate3d on;

頭皮メッシュから仮想球を作成
頭皮メッシュから仮想球を作成します。
figure('color',[1,1,1],'position',[50,50,500,50]); st='$$x^2+y^2+z^2+ax+by+cz+d=0$$'; text(-0.1,0.5,st,'interpreter','latex','fontsize',18);axis off;
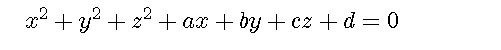
%という球を仮定します。変形します。 figure('color',[1,1,1],'position',[50,50,500,50]); st='$$ax+by+cz+d=-(x^2+y^2+z^2)$$'; text(-0.1,0.5,st,'interpreter','latex','fontsize',18);axis off;
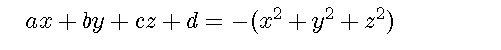
%x,y,zは頭皮の座標になります。a,b,c,dは行列の割り算で簡単に求まります。 % 球の中心は figure('color',[1,1,1],'position',[50,50,200,100]); st='$$\left(-\frac{a}{2},-\frac{b}{2},-\frac{c}{2}\right)$$'; text(-0.1,0.5,st,'interpreter','latex','fontsize',18);axis off;
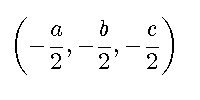
となります。また半径は
figure('color',[1,1,1],'position',[50,50,300,100]); st='$$\sqrt{\frac{a^2}{4}+\frac{b^2}{4}+\frac{c^2}{4}-d}$$'; text(-0.1,0.5,st,'interpreter','latex','fontsize',18);axis off;
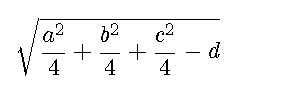
となります。 実際に試してみます。
figure('color',[1,1,1]); p=hmesh.vertices; plot3(p(:,1),p(:,2),p(:,3),'r.');hold on; axis equal;axis tight;axis off; q=[p,ones(size(p,1),1)]\(-sum(p.^2,2)); c0=-q(1:3)/2; r=sqrt(sum(c0.^2)-q(4)); [sx,sy,sz]=sphere(20); sx=sx*r+c0(1); sy=sy*r+c0(2); sz=sz*r+c0(3); h0=surf(sx,sy,sz,'facecolor',[1,1,0],'facealpha',0.2,'edgecolor','none'); rotate3d on;
