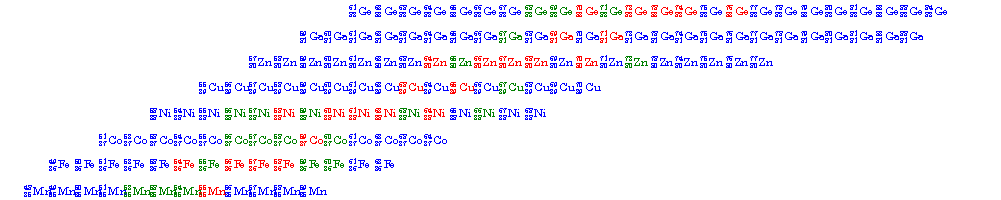Contents
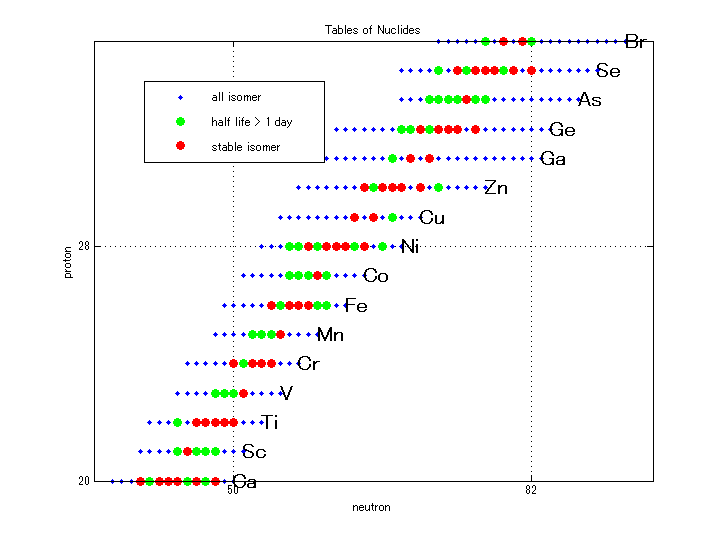
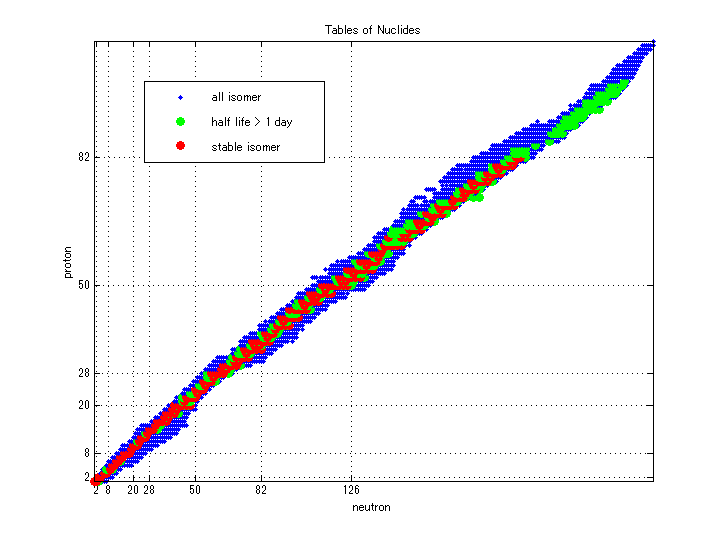
核図表 tables of nuclides
元素の同位体を含めた図です。 赤は安定同位体、緑は半減期が1日以上の不安定同位体です。2,8,20,28,50,82,126は原子核の魔法数です。
close all; n=0; n=n+1;Z{n}='H'; Isomer{n}=1:7; n=n+1;Z{n}='He';Isomer{n}=2:10; n=n+1;Z{n}='Li';Isomer{n}=4:12; n=n+1;Z{n}='Be';Isomer{n}=5:14; n=n+1;Z{n}='B';Isomer{n}=7:19; n=n+1;Z{n}='C';Isomer{n}=8:22; n=n+1;Z{n}='N';Isomer{n}=10:24; n=n+1;Z{n}='O';Isomer{n}=12:26; n=n+1;Z{n}='F';Isomer{n}=14:29; n=n+1;Z{n}='Ne';Isomer{n}=15:32; n=n+1;Z{n}='Na';Isomer{n}=18:35; n=n+1;Z{n}='Mg';Isomer{n}=20:38; n=n+1;Z{n}='Al';Isomer{n}=21:41; n=n+1;Z{n}='Si';Isomer{n}=22:42; n=n+1;Z{n}='P';Isomer{n}=24:46; n=n+1;Z{n}='S';Isomer{n}=29:45; n=n+1;Z{n}='Cl';Isomer{n}=31:46; n=n+1;Z{n}='Ar';Isomer{n}=33:47; n=n+1;Z{n}='K';Isomer{n}=35:50; n=n+1;Z{n}='Ca';Isomer{n}=37:50; n=n+1;Z{n}='Sc';Isomer{n}=40:51; n=n+1;Z{n}='Ti';Isomer{n}=41:53; n=n+1;Z{n}='V';Isomer{n}=44:55; n=n+1;Z{n}='Cr';Isomer{n}=45:57; n=n+1;Z{n}='Mn';Isomer{n}=48:59; n=n+1;Z{n}='Fe';Isomer{n}=49:62; n=n+1;Z{n}='Co';Isomer{n}=51:64; n=n+1;Z{n}='Ni';Isomer{n}=53:68; n=n+1;Z{n}='Cu';Isomer{n}=55:70; n=n+1;Z{n}='Zn';Isomer{n}=57:77; n=n+1;Z{n}='Ga';Isomer{n}=59:83; n=n+1;Z{n}='Ge';Isomer{n}=61:84; n=n+1;Z{n}='As';Isomer{n}=68:87; n=n+1;Z{n}='Se';Isomer{n}=68:89; n=n+1;Z{n}='Br';Isomer{n}=72:92; n=n+1;Z{n}='Kr';Isomer{n}=[72:95,97]; n=n+1;Z{n}='Rb';Isomer{n}=74:99; n=n+1;Z{n}='Sr';Isomer{n}=77:99; n=n+1;Z{n}='Y';Isomer{n}=[81:100,102]; n=n+1;Z{n}='Zr';Isomer{n}=81:102; n=n+1;Z{n}='Nb';Isomer{n}=[84,86:106]; n=n+1;Z{n}='Mo';Isomer{n}=87:108; n=n+1;Z{n}='Tc';Isomer{n}=90:110; n=n+1;Z{n}='Ru';Isomer{n}=92:113; n=n+1;Z{n}='Rh';Isomer{n}=95:114; n=n+1;Z{n}='Pd';Isomer{n}=97:118; n=n+1;Z{n}='Ag';Isomer{n}=99:123; n=n+1;Z{n}='Cd';Isomer{n}=[100:122,124]; n=n+1;Z{n}='In';Isomer{n}=104:132; n=n+1;Z{n}='Sn';Isomer{n}=107:134; n=n+1;Z{n}='Sb';Isomer{n}=110:136; n=n+1;Z{n}='Te';Isomer{n}=[107:109,111:138]; n=n+1;Z{n}='I';Isomer{n}=115:142; n=n+1;Z{n}='Xe';Isomer{n}=[113,115:145]; n=n+1;Z{n}='Cs';Isomer{n}=116:146; n=n+1;Z{n}='Ba';Isomer{n}=[119,121:146]; n=n+1;Z{n}='La';Isomer{n}=125:148; n=n+1;Z{n}='Ce';Isomer{n}=129:151; n=n+1;Z{n}='Pr';Isomer{n}=132:151; n=n+1;Z{n}='Nd';Isomer{n}=[134:152,154]; n=n+1;Z{n}='Pm';Isomer{n}=137:154; n=n+1;Z{n}='Sm';Isomer{n}=137:157; n=n+1;Z{n}='Eu';Isomer{n}=139:160; n=n+1;Z{n}='Gd';Isomer{n}=142:162; n=n+1;Z{n}='Tb';Isomer{n}=146:164; n=n+1;Z{n}='Dy';Isomer{n}=147:167; n=n+1;Z{n}='Ho';Isomer{n}=150:170; n=n+1;Z{n}='Er';Isomer{n}=150:173; n=n+1;Z{n}='Tm';Isomer{n}=[151,153:176]; n=n+1;Z{n}='Yb';Isomer{n}=[154:158,160:178]; n=n+1;Z{n}='Lu';Isomer{n}=[155,156,161,162,164:180]; n=n+1;Z{n}='Hf';Isomer{n}=[157:161,166:185]; n=n+1;Z{n}='Ta';Isomer{n}=166:186; n=n+1;Z{n}='W';Isomer{n}=[162:166,170:190]; n=n+1;Z{n}='Re';Isomer{n}=[170,172,174:192]; n=n+1;Z{n}='Os';Isomer{n}=169:196; n=n+1;Z{n}='Ir';Isomer{n}=171:198; n=n+1;Z{n}='Pt';Isomer{n}=173:201; n=n+1;Z{n}='Au';Isomer{n}=[175:179,181:204]; n=n+1;Z{n}='Hg';Isomer{n}=177:206; n=n+1;Z{n}='Tl';Isomer{n}=184:210; n=n+1;Z{n}='Pb';Isomer{n}=185:214; n=n+1;Z{n}='Bi';Isomer{n}=189:215; n=n+1;Z{n}='Po';Isomer{n}=193:218; n=n+1;Z{n}='At';Isomer{n}=194:219; n=n+1;Z{n}='Rn';Isomer{n}=200:226; n=n+1;Z{n}='Fr';Isomer{n}=203:229; n=n+1;Z{n}='Ra';Isomer{n}=206:230; n=n+1;Z{n}='Ac';Isomer{n}=209:232; n=n+1;Z{n}='Th';Isomer{n}=213:236; n=n+1;Z{n}='Pa';Isomer{n}=[216,222:238]; n=n+1;Z{n}='U';Isomer{n}=226:240; n=n+1;Z{n}='Np';Isomer{n}=228:241; n=n+1;Z{n}='Pu';Isomer{n}=232:246; n=n+1;Z{n}='Am';Isomer{n}=[232,234:247]; n=n+1;Z{n}='Cm';Isomer{n}=236:251; n=n+1;Z{n}='Bk';Isomer{n}=239:254; n=n+1;Z{n}='Cf';Isomer{n}=240:256; n=n+1;Z{n}='Es';Isomer{n}=241:257; n=n+1;Z{n}='Fm';Isomer{n}=242:259; n=n+1;Z{n}='Md';Isomer{n}=248:260; n=n+1;Z{n}='No';Isomer{n}=250:262; n=n+1;Z{n}='Lr';Isomer{n}=252:263; n=n+1;Z{n}='Rf';Isomer{n}=253:264; n=n+1;Z{n}='Db';Isomer{n}=255:265; n=n+1;Z{n}='Sg';Isomer{n}=258:266; n=n+1;Z{n}='Bh';Isomer{n}=260:267; n=n+1;Z{n}='Hs';Isomer{n}=263:269; n=n+1;Z{n}='Mt';Isomer{n}=265:271; n=n+1;Z{n}='Ds';Isomer{n}=267:272; n=n+1;Z{n}='Rg';Isomer{n}=272; % 安定同位体 n=0; n=n+1;Isomer1{n}=1:2; n=n+1;Isomer1{n}=3:4; n=n+1;Isomer1{n}=6:7; n=n+1;Isomer1{n}=9; n=n+1;Isomer1{n}=10:11; n=n+1;Isomer1{n}=12:13; n=n+1;Isomer1{n}=14:15; n=n+1;Isomer1{n}=16:18; n=n+1;Isomer1{n}=19; n=n+1;Isomer1{n}=20:22; n=n+1;Isomer1{n}=23; n=n+1;Isomer1{n}=24:26; n=n+1;Isomer1{n}=27; n=n+1;Isomer1{n}=28:30; n=n+1;Isomer1{n}=31; n=n+1;Isomer1{n}=[32:34,36]; n=n+1;Isomer1{n}=[35,37]; n=n+1;Isomer1{n}=[36,38,40]; n=n+1;Isomer1{n}=[39,41]; n=n+1;Isomer1{n}=[40,42:44,46,48]; n=n+1;Isomer1{n}=45; n=n+1;Isomer1{n}=46:50; n=n+1;Isomer1{n}=51; n=n+1;Isomer1{n}=[50,52:54]; n=n+1;Isomer1{n}=55; n=n+1;Isomer1{n}=[54,56:58]; n=n+1;Isomer1{n}=59; n=n+1;Isomer1{n}=[58,60:62,64]; n=n+1;Isomer1{n}=[63,65]; n=n+1;Isomer1{n}=[64,66:68,70]; n=n+1;Isomer1{n}=[69,71]; n=n+1;Isomer1{n}=[70,72:74,76]; n=n+1;Isomer1{n}=75; n=n+1;Isomer1{n}=[74,76:78,80,82]; n=n+1;Isomer1{n}=[79,81]; n=n+1;Isomer1{n}=[78,80,82:84,86]; n=n+1;Isomer1{n}=85; n=n+1;Isomer1{n}=[84,86:88]; n=n+1;Isomer1{n}=89; n=n+1;Isomer1{n}=[90:92,94,96]; n=n+1;Isomer1{n}=93; n=n+1;Isomer1{n}=[92,94:98,100]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[96,98:102,104]; n=n+1;Isomer1{n}=103; n=n+1;Isomer1{n}=[102,104:106,108,110]; n=n+1;Isomer1{n}=[107,109]; n=n+1;Isomer1{n}=[106,108,110:112,114,116]; n=n+1;Isomer1{n}=113; n=n+1;Isomer1{n}=[112,114:120,122,124]; n=n+1;Isomer1{n}=[121,123]; n=n+1;Isomer1{n}=[120,122,124:126,128,130]; n=n+1;Isomer1{n}=127; n=n+1;Isomer1{n}=[124,126,128:132,134,136]; n=n+1;Isomer1{n}=133; n=n+1;Isomer1{n}=[130,132,134:138]; n=n+1;Isomer1{n}=139; n=n+1;Isomer1{n}=[136,138,140]; n=n+1;Isomer1{n}=141; n=n+1;Isomer1{n}=[142:146,148,150]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[144,150,152,154]; n=n+1;Isomer1{n}=[151,153]; n=n+1;Isomer1{n}=[154:158,160]; n=n+1;Isomer1{n}=159; n=n+1;Isomer1{n}=[158,160:164]; n=n+1;Isomer1{n}=165; n=n+1;Isomer1{n}=[162,164,166:168,170]; n=n+1;Isomer1{n}=169; n=n+1;Isomer1{n}=[168,170:174,176]; n=n+1;Isomer1{n}=175; n=n+1;Isomer1{n}=176:180; n=n+1;Isomer1{n}=[180,181];%maybe 180,too n=n+1;Isomer1{n}=[180,182:184,186]; n=n+1;Isomer1{n}=185; n=n+1;Isomer1{n}=[184,187:190,192]; n=n+1;Isomer1{n}=[191,193]; n=n+1;Isomer1{n}=[192,194:196,198]; n=n+1;Isomer1{n}=197; n=n+1;Isomer1{n}=[196,198:202,204]; n=n+1;Isomer1{n}=[203,205]; n=n+1;Isomer1{n}=206:208; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; n=n+1;Isomer1{n}=[]; % 半減期1日以上 n=0; n=n+1;Isomer2{n}=3; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[7,10]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=14; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=22; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=26; n=n+1;Isomer2{n}=32; n=n+1;Isomer2{n}=[32,33]; n=n+1;Isomer2{n}=35; n=n+1;Isomer2{n}=36; n=n+1;Isomer2{n}=[37,39,42]; n=n+1;Isomer2{n}=40; n=n+1;Isomer2{n}=[41,45,47]; n=n+1;Isomer2{n}=[44,46:48]; n=n+1;Isomer2{n}=44; n=n+1;Isomer2{n}=48:50; n=n+1;Isomer2{n}=51; n=n+1;Isomer2{n}=52:54; n=n+1;Isomer2{n}=[55,59,60]; n=n+1;Isomer2{n}=[56:58,60]; n=n+1;Isomer2{n}=[56,57,59,63,66]; n=n+1;Isomer2{n}=67; n=n+1;Isomer2{n}=[65,72]; n=n+1;Isomer2{n}=67; n=n+1;Isomer2{n}=[68,69,71]; n=n+1;Isomer2{n}=[71:74,76,77]; n=n+1;Isomer2{n}=[72,75,79]; n=n+1;Isomer2{n}=[77,82]; n=n+1;Isomer2{n}=[79,81,85]; n=n+1;Isomer2{n}=[83,84,86,87]; n=n+1;Isomer2{n}=[82,83,85,89,90]; n=n+1;Isomer2{n}=[87,88,90,91]; n=n+1;Isomer2{n}=[88,89,93,95]; n=n+1;Isomer2{n}=[91,92,94,95]; n=n+1;Isomer2{n}=[93,99]; n=n+1;Isomer2{n}=96:99; n=n+1;Isomer2{n}=[97,103,105,106]; n=n+1;Isomer2{n}=[99,101,102,105]; n=n+1;Isomer2{n}=[100,103,107]; n=n+1;Isomer2{n}=[105,111]; n=n+1;Isomer2{n}=[109,113,115]; n=n+1;Isomer2{n}=[111,115]; n=n+1;Isomer2{n}=[113,121,123,125,126]; n=n+1;Isomer2{n}=[119,122,124:127]; n=n+1;Isomer2{n}=[118,121,123,132]; n=n+1;Isomer2{n}=[124:126,129,131]; n=n+1;Isomer2{n}=[127,133]; n=n+1;Isomer2{n}=[129,131,132,134:137]; n=n+1;Isomer2{n}=[128,131,133,140]; n=n+1;Isomer2{n}=[137,138,140]; n=n+1;Isomer2{n}=[134,137,139,141:144]; n=n+1;Isomer2{n}=143; n=n+1;Isomer2{n}=[140,144,147]; n=n+1;Isomer2{n}=[143:149,151]; n=n+1;Isomer2{n}=[145:149,151,153]; n=n+1;Isomer2{n}=[145:149,152,154:156]; n=n+1;Isomer2{n}=146:153; n=n+1;Isomer2{n}=[153,155:158,160,161]; n=n+1;Isomer2{n}=[154,156,159,166]; n=n+1;Isomer2{n}=[163,166]; n=n+1;Isomer2{n}=[160,169,172]; n=n+1;Isomer2{n}=[165,167,168,170:172]; n=n+1;Isomer2{n}=[166,169,175]; n=n+1;Isomer2{n}=[169:174,176,177]; n=n+1;Isomer2{n}=[178,181,185,188]; n=n+1;Isomer2{n}=[177,179,180,182,183]; n=n+1;Isomer2{n}=[178,181,185,188]; n=n+1;Isomer2{n}=[182:184,186,187,189]; n=n+1;Isomer2{n}=[185,186,193,194]; n=n+1;Isomer2{n}=[188:190,192]; n=n+1;Isomer2{n}=[188,190,191,193]; n=n+1;Isomer2{n}=[194:196,198,199]; n=n+1;Isomer2{n}=[194,197,203]; n=n+1;Isomer2{n}=[200:202,204]; n=n+1;Isomer2{n}=[202:205,210]; n=n+1;Isomer2{n}=[205:207,209,210]; n=n+1;Isomer2{n}=[205:207,209,210]; n=n+1;Isomer2{n}=215; n=n+1;Isomer2{n}=222; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[223:226,228]; n=n+1;Isomer2{n}=225:227; n=n+1;Isomer2{n}=[227:232,234]; n=n+1;Isomer2{n}=229:234; n=n+1;Isomer2{n}=230:238; n=n+1;Isomer2{n}=234:239; n=n+1;Isomer2{n}=[236:242,244,246]; n=n+1;Isomer2{n}=[240,241,243]; n=n+1;Isomer2{n}=[240:248,250]; n=n+1;Isomer2{n}=245:249; n=n+1;Isomer2{n}=[246,248:254]; n=n+1;Isomer2{n}=251:255; n=n+1;Isomer2{n}=[252,253,257]; n=n+1;Isomer2{n}=258; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; n=n+1;Isomer2{n}=[]; figure('name','tables of nuclides','numbertitle','off','color',[1,1,1]); set(gcf,'position',[50,50,720,540]); for n=1:length(Isomer) plot(Isomer{n},n*ones(1,length(Isomer{n})),'b.','tag','isomer'); if n==1;hold on;end; plot(Isomer2{n},n*ones(1,length(Isomer2{n})),'go','tag','isomer2'); plot(Isomer1{n},n*ones(1,length(Isomer1{n})),'ro','tag','isomer1'); if n==1; L=legend('all isomer','half life > 1 day','stable isomer'); set(L,'position',[0.2,0.7,0.25,0.15]); end; end; set(findobj(gcf,'tag','isomer2'),'MarkerFacecolor',[0,1,0],'MarkerEdgeColor',[0,1,0]); set(findobj(gcf,'tag','isomer1'),'MarkerFaceColor',[1,0,0],'MarkerEdgeColor',[1,0,0]); title('Tables of Nuclides'); ylabel('proton');xlabel('neutron'); tick=[2,8,20,28,50,82,126]; set(gca,'xtick',tick,'ytick',tick);grid on; axis tight;
Co60あたりの核図表
Co60あたりを拡大したものと、Latexを使って元素記号で表示したものを示します。
for n=20:35 text(Isomer{n}(end),n,Z{n},'FontSize',15,'FontWeight','bold'); end; set(gca,'ylim',[20,35],'xlim',[35,95]); figure('color',[1,1,1],'position',[50,50,1000,200]); for n=25:32 for m=1:length(Isomer{n}) N=Isomer{n}(m); st=sprintf('$$ ^{%d} _{%d}$$',N,n); h=text(N,n,[st,Z{n}],'interpreter','latex','color',[0,0,1]);hold on; if ismember(N,Isomer2{n});set(h,'color',[0,0.5,0]);end; if ismember(N,Isomer1{n});set(h,'color',[1,0,0]);end; end; end; set(gca,'ylim',[25,32],'xlim',[49,85],'position',[0.05,0.05,0.9,0.9]); axis off;