Contents
球面調和関数の式
球面調和関数は球座標版のフーリエ変換です。 式の中にルジャンドル(Legendre)陪関数を含みます。 ルジャンドル陪関数はルジャンドル多項式を含みます。 式は以下の通り複雑です。
close all;clear all; fs='FontSize'; figure('color',[1,1,1],'position',[50,50,800,400]); st1='$$Y ^m _l (\theta, \phi)=(-1)^{(m+|m|)/2} \sqrt{\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}}'; st2=' P^{|m|}_l (cos\theta) e^{im\phi}$$'; st3='$$P^{m}_{l}(x)=(-1)^m(1-x^2)^{m/2}\frac{d^m}{dx^m}P_l(x)$$'; st4='$$P_{l}(x)=\frac{1}{2^ll!}\frac{d^l}{dl^l}\left[(x^2-1)^l\right]$$'; text(-0.1,0.9,[st1,st2],'interpreter','latex',fs,20); text(-0.1,0.6,st3,'interpreter','latex',fs,20); text(-0.1,0.3,st4,'interpreter','latex',fs,20); axis tight;axis off; figure('color',[1,1,1],'position',[50,50,800,800]'); st{1}='$$Y^0_0(x)=\frac{1}{2}\sqrt{\frac{1}{\pi}}$$'; st{2}='$$Y^0_1(x)=\frac{1}{2}\sqrt{\frac{3}{\pi}}\cdot\cos\theta$$'; st{3}='$$Y^{\mp1}_1(x)=\pm\frac{-1}{2}\sqrt{\frac{3}{2\pi}}\cdot e^{\mp i\phi}\cdot\sin\theta$$'; st{4}='$$Y^0_2(x)=\frac{1}{4}\sqrt{\frac{5}{\pi}}\cdot(3\cos^2\theta-1)$$'; st{5}='$$Y^{\mp1}_2(x)=\pm\frac{-1}{2}\sqrt{\frac{15}{2\pi}}\cdot e^{\mp i\phi}\cdot\sin\theta\cdot\cos\theta$$'; st{6}='$$Y^{\mp2}_2(x)=\frac{1}{4}\sqrt{\frac{15}{2\pi}}\cdot e^{\mp2i\phi}\cdot\sin^2\theta$$'; st{7}='$$Y^0_3(x)=\frac{1}{4}\sqrt{\frac{7}{\pi}}\cdot (5\cos^3\theta-3\cos\theta)$$'; st{8}='$$Y^{\mp1}_3(x)=\pm\frac{1}{8}\sqrt{\frac{21}{\pi}}\cdot e^{\mp i\phi}\cdot (5\cos^2\theta-1)$$'; st{9}='$$Y^{\mp2}_3(x)=\frac{1}{4}\sqrt{\frac{105}{2\pi}}\cdot e^{\mp2i\phi}\cdot\sin^2\theta\cdot\cos\theta$$'; st{10}='$$Y^{\mp3}_3(x)=\pm\frac{1}{8}\sqrt{\frac{35}{\pi}}\cdot e^{\mp3i\phi}\cdot\sin^3\theta$$'; for n=1:length(st) text(-0.1,1.15-0.12*n,st{n},'interpreter','latex','FontSize',18); end; axis off;
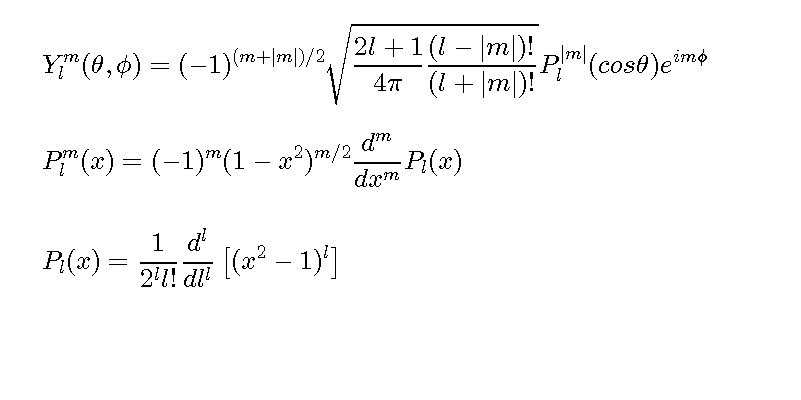
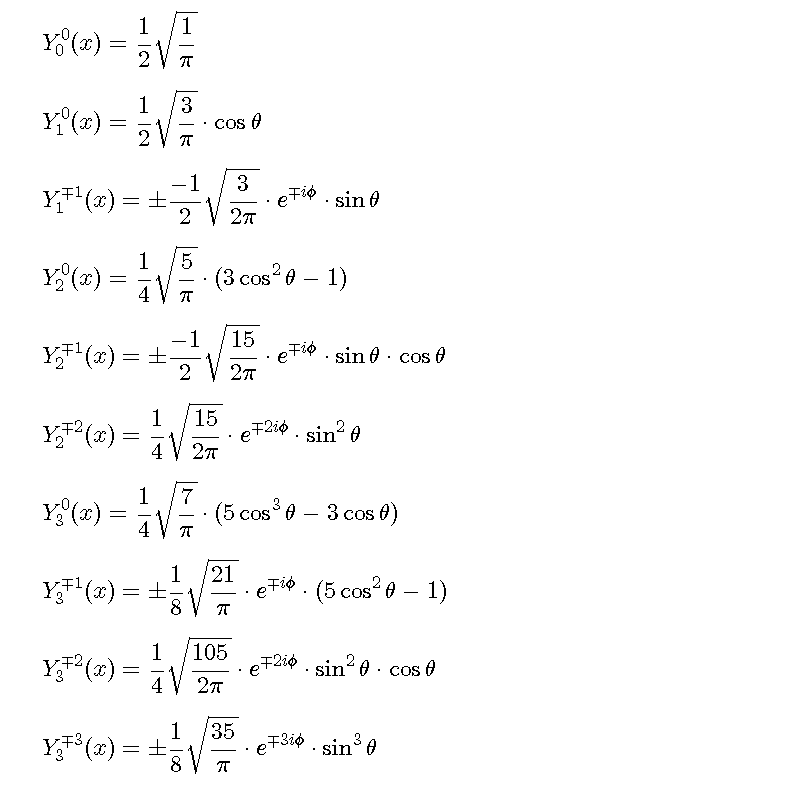
ルジャンドル陪関数(随伴関数)legendre
MATLABには幸いルジャンドル陪関数の関数legendreが用意してあります。 Pml=lengendre((l,~)とするとmの値を0~lに変化させた結果が返ってきます。 ルジャンドル陪関数は直交性があり、これを含む球面調和関数も直交性があります。
close all;clear; seg=36; x=linspace(-1,1,seg+1); figure('color',[1,1,1],'InvertHardCopy','off'); P0l=[]; for m=0:6 Pml=legendre(abs(m),x); P0l=[P0l;Pml(1,:)]; end; plot(x,P0l);hold on; L=legend('P_0^0','P_1^0','P_2^0','P_3^0','P_4^0','P_5^0','P_6^0'); set(L,'location','bestoutside'); axis tight; title('Legendre function'); seg=36; x=linspace(-1,1,seg+1); figure('color',[1,1,1],'InvertHardCopy','off'); for l=0:5; subplot(2,3,l+1); Pml=legendre(l,x); plot(x,Pml);hold on; axis tight; st=[]; for m=0:l st=[st,sprintf('P_%d^%d ',l,m)]; end; title(st); end;
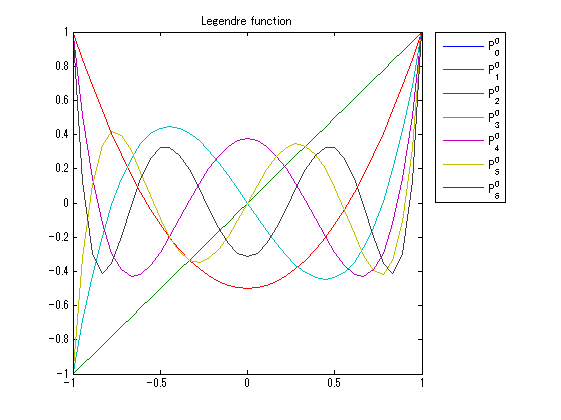
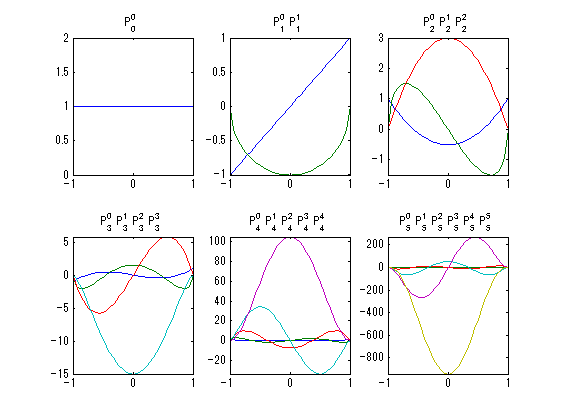
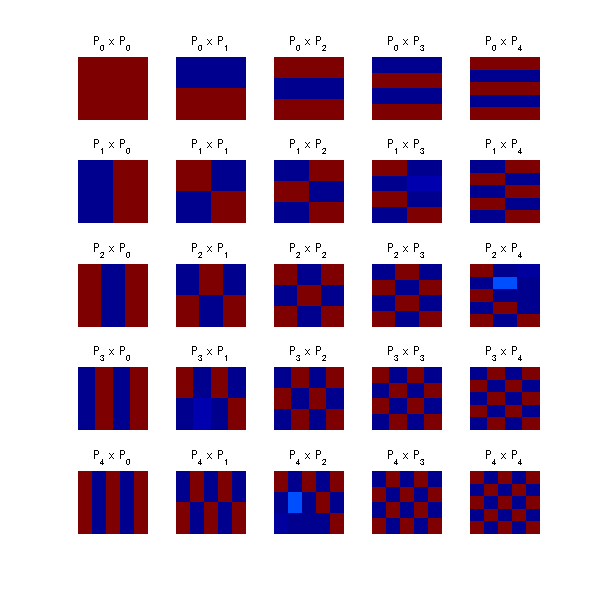
ルジャンドル陪関数の直交性の検討
m==m以外の時は内積はゼロになります。 式レベルで証明されています。 検討してみました。 青がゼロです。市松模様みたいになってしまいました。 丸めなどの計算誤差のせいなんだろうか?
close all; figure('color',[1,1,1],'position',[50,50,600,600]); seg=100;N=4; t=linspace(-1,1,seg); for x=0:N Px=legendre(x,t); for y=0:N K=legendre(y,t)*Px'; subplot(N+1,N+1,x*(N+1)+y+1); imagesc(abs(K)); title(sprintf('P_%d x P_%d',x,y)); axis off; end; end; set(findobj(gcf,'type','axes'),'clim',[0,1]);
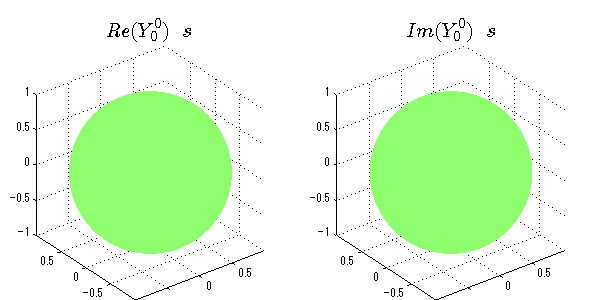
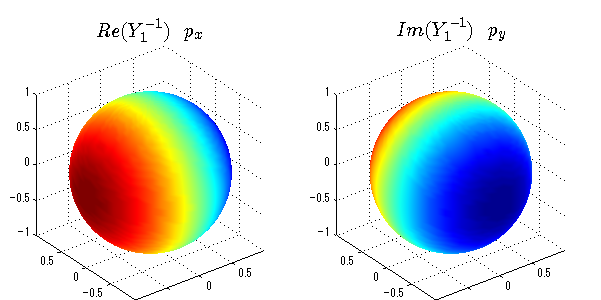
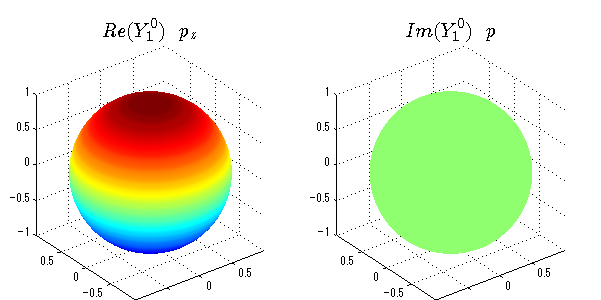
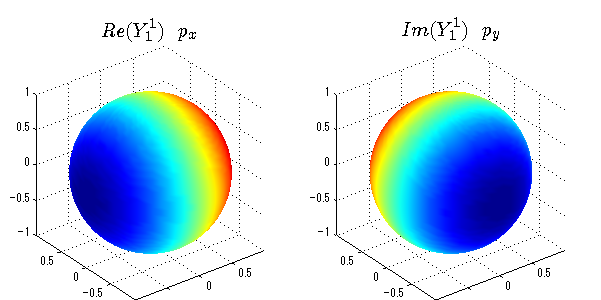
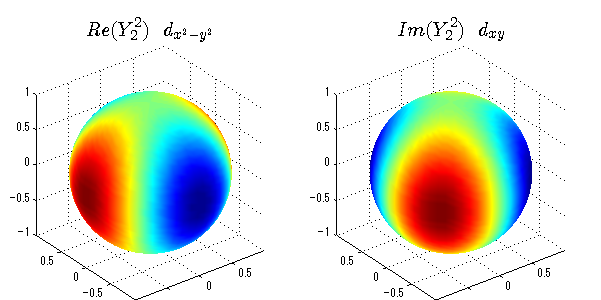
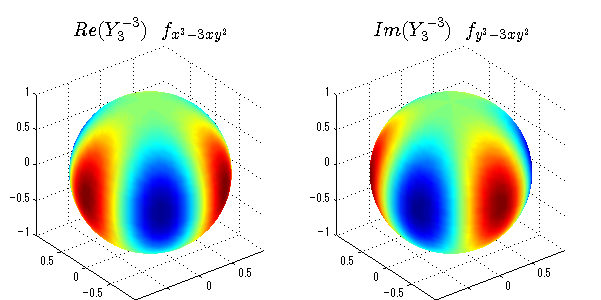
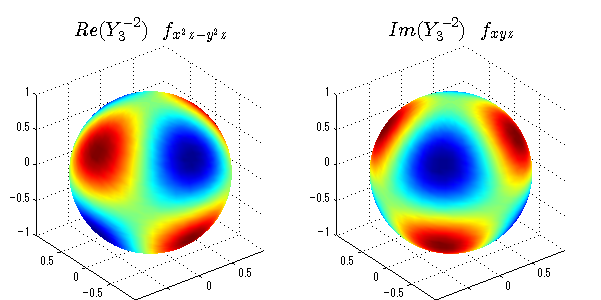
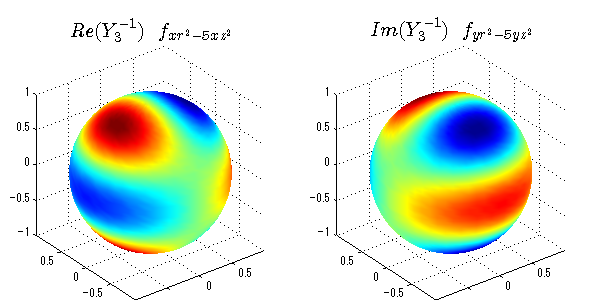
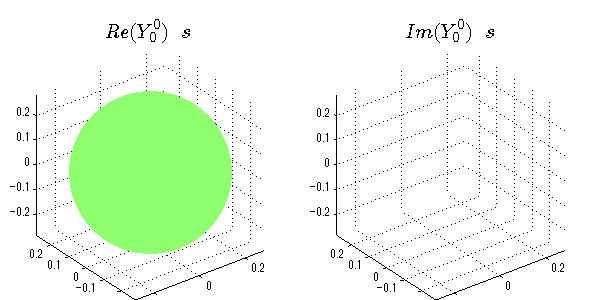
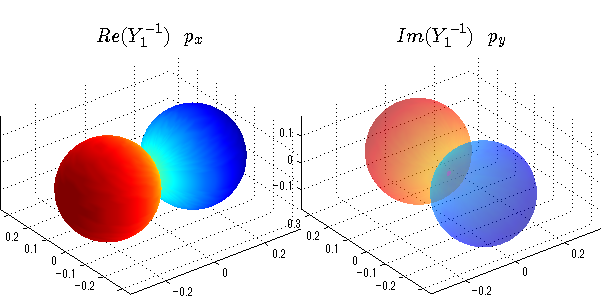
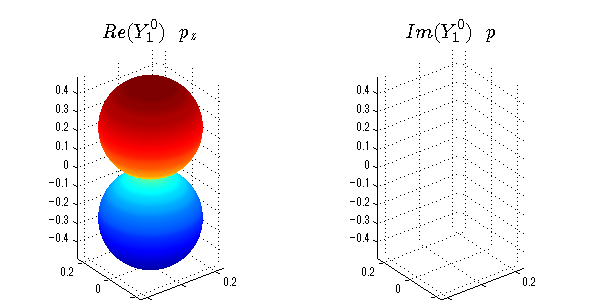
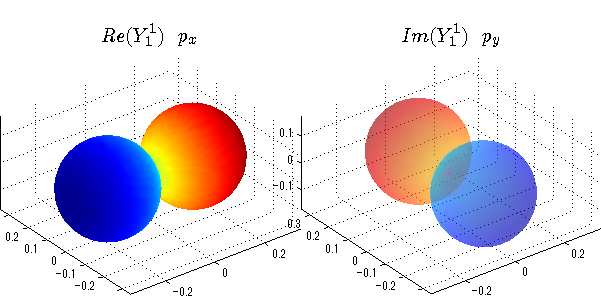
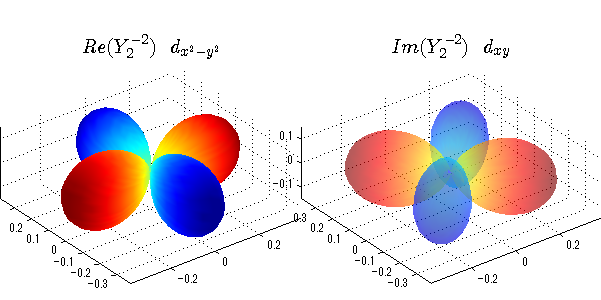
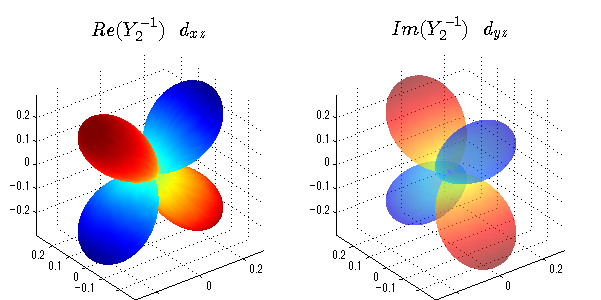
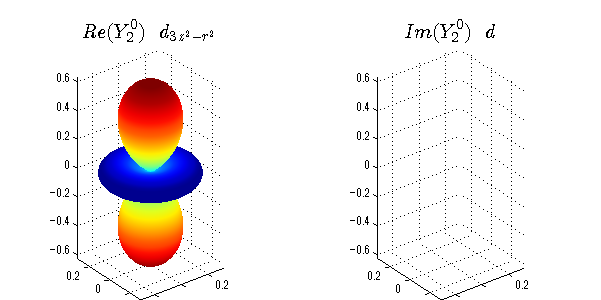
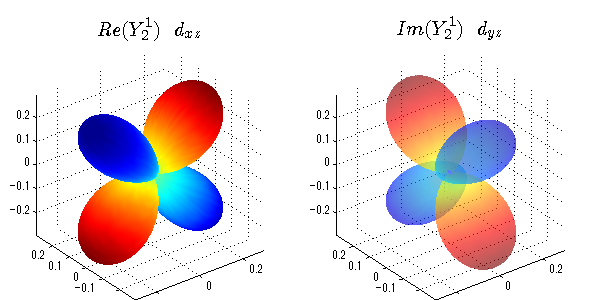
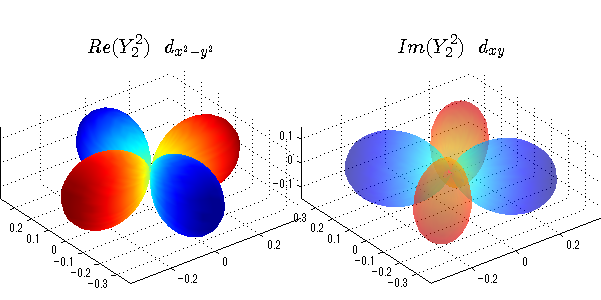
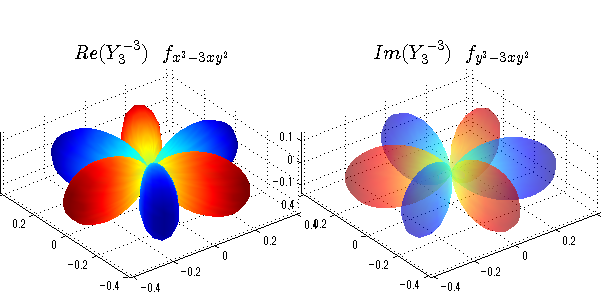
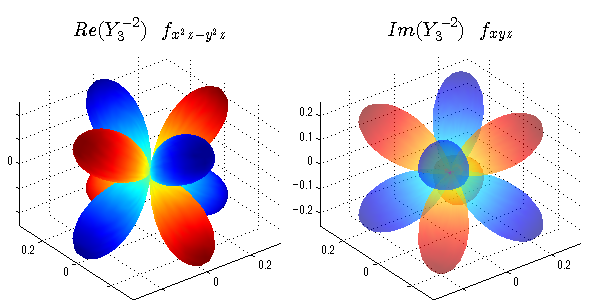
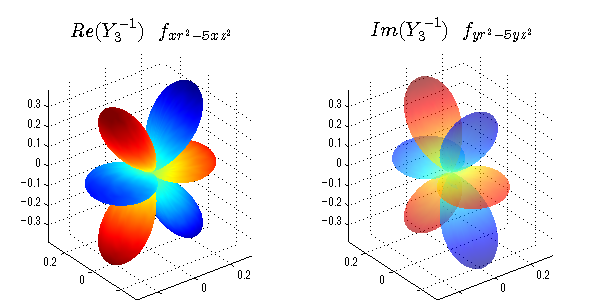
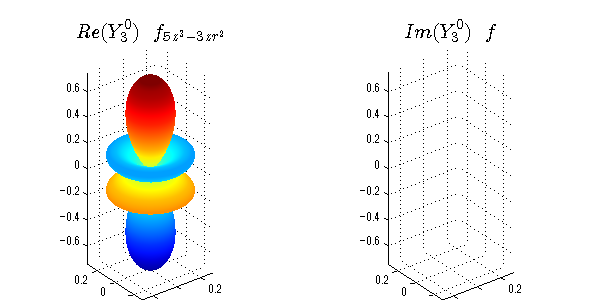
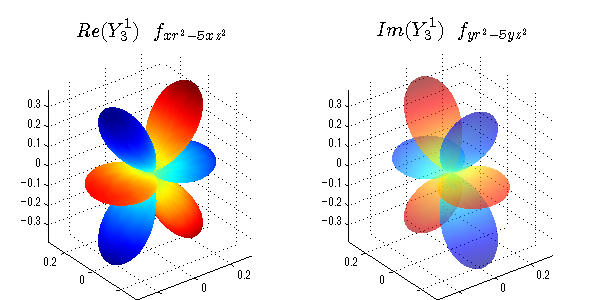
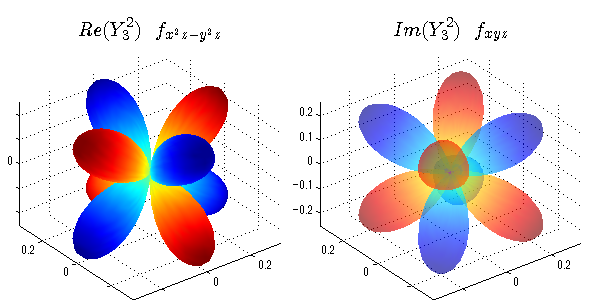
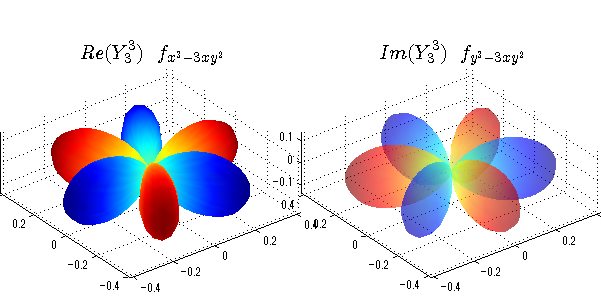
球面調和関数の作成 半径=1で実数・虚数別の球面表示
上記のlegendre関数を使って球面調和関数を作成できます。 Yの下段はl、上段はmです。lを0,1,2...と変化させてみました。 lにはs(harp),p(rinciple),d(iffuse),f(aint),g,h,i,・・・といった名前がついています。 本来複素表示なのですが、実数部分と虚数部分に分けて表示してみました。 zは軸方向、xは実数方向、yは虚数方向です。 中心からの距離=半径は1で統一しました。色は、実数部分、虚数部分の大きさを反映させました。 左が実数部分で、右が虚数部分です。m=0のとき、虚数部分はゼロとなります。 この図が一番わかりやすいと思います。要するにlは緯度方向の波の数、mは経度方向の波の数です。
close all;clear; N=5; seg=64; theta=linspace(0,pi,seg); phi=linspace(0,2*pi,seg); Theta=theta'*ones(1,seg); Phi=ones(seg,1)*phi; x=sin(Theta).*cos(Phi); y=sin(Theta).*sin(Phi); z=cos(Theta); for l=0:N; L=legendre(l,cos(theta)); for m=-l:l; am=abs(m); LL=L(abs(m)+1,:); c=(-1)^((m+am)/2)*sqrt((2*l+1)/(4*pi)*factorial(l-am)/factorial(l+am))*LL'*exp(1i*m*phi); figure('color',[1,1,1],'inverthardcopy','off','position',[50,50,600,300]); for mm=1:2 subplot('position',[(mm-1)*0.5,0,0.5,0.85]); if mm==1;cc=real(c);else cc=imag(c);end; h=surf(x,y,z,cc); set(h,'FaceColor','interp','EdgeColor','none'); grid on; daspect([1,1,1]); axis tight; rotate3d on; if mm==1 st1=sprintf('Re(Y_%d^{%d})',l,m); else st1=sprintf('Im(Y_%d^{%d})',l,m); end; switch l case 0;st2='s';st3=''; case 1; st2='p'; switch m; case {-1,1};st3='_x';if mm==2;st3='_y';end; case 0;st3='_z'; if mm==2;st3=''; end; end; case 2; st2='d_{'; switch m; case {-2,2};st3='x^2-y^2}';if mm==2;st3='xy}';end; case {-1,1};st3='xz}'; if mm==2;st3='yz}';end; case 0;st3='3z^2-r^2}'; if mm==2;st3='}';end; end; case 3; st2='f_{'; switch m; case {-3,3};st3='x^3-3xy^2}'; if mm==2;st3='y^3-3xy^2}';end; case {-2,2};st3='x^2z-y^2z}'; if mm==2;st3='xyz}';end; case {-1,1};st3='xr^2-5xz^2}';if mm==2;st3='yr^2-5yz^2}';end; case 0;st3='5z^3-3zr^2}'; if mm==2;st3='}';end; end; case 4;st2='g';st3=''; case 5;st2='h';st3=''; end; title(['$$',st1,'\ \ ',st2,st3,'$$'],'interpreter','latex','FontSize',15); end; end; end;
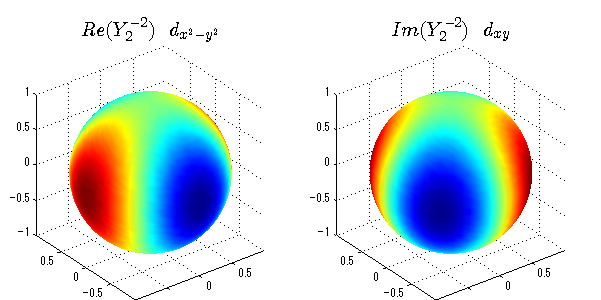
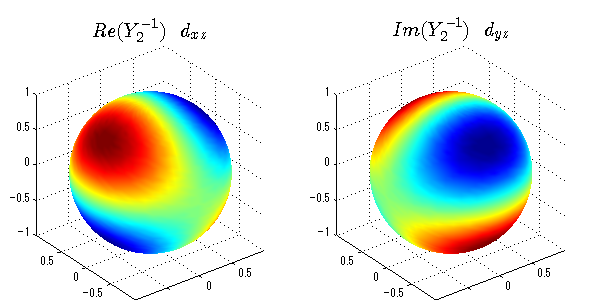
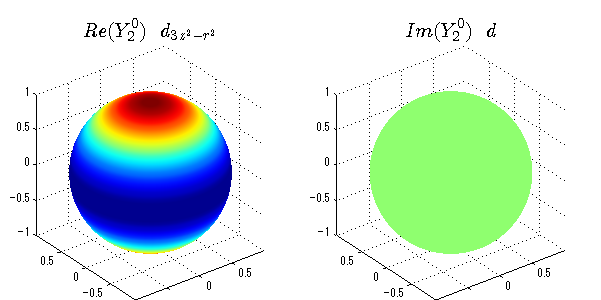
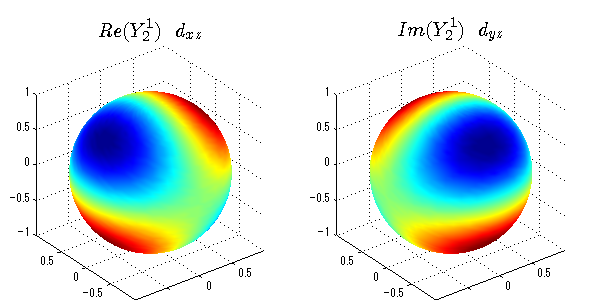
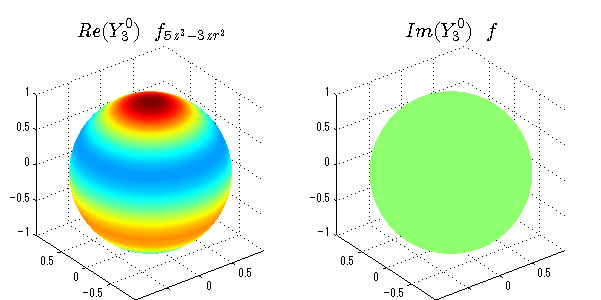
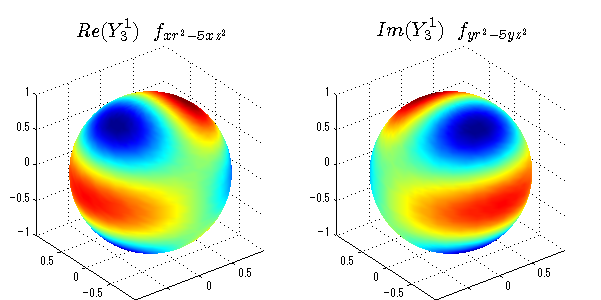
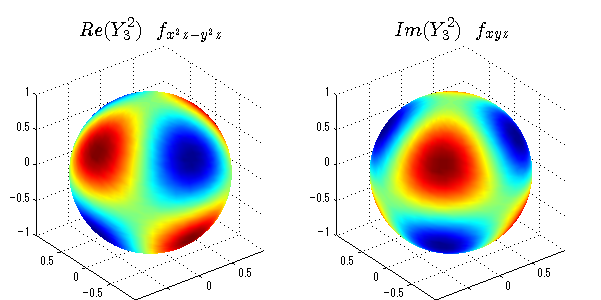
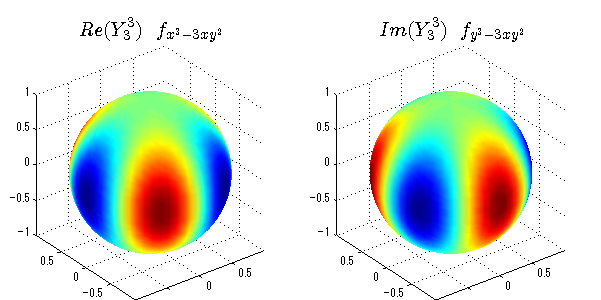
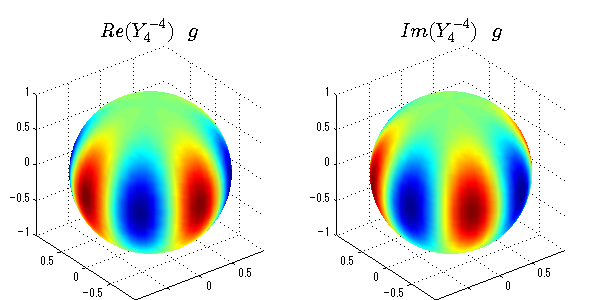
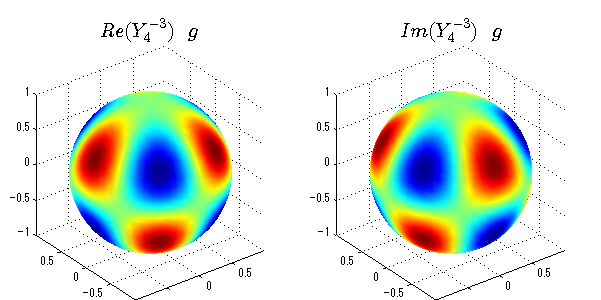
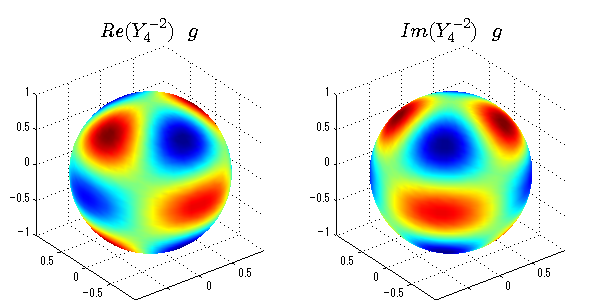
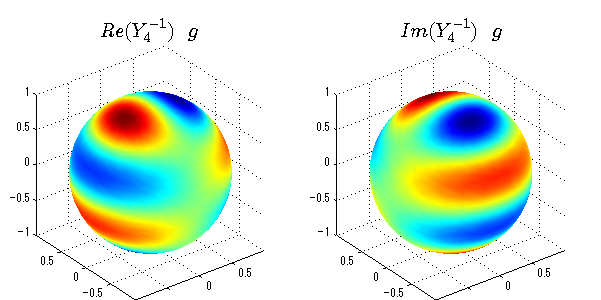
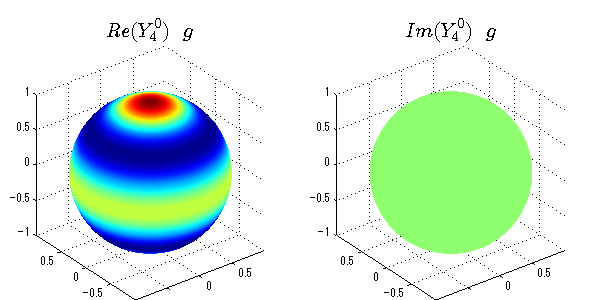
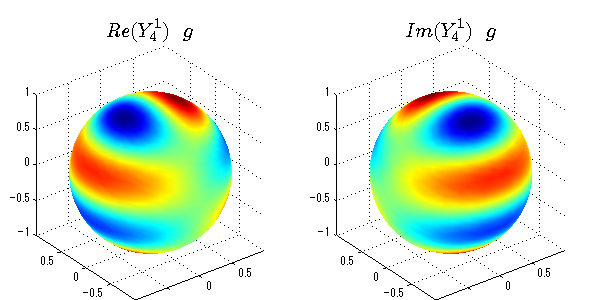
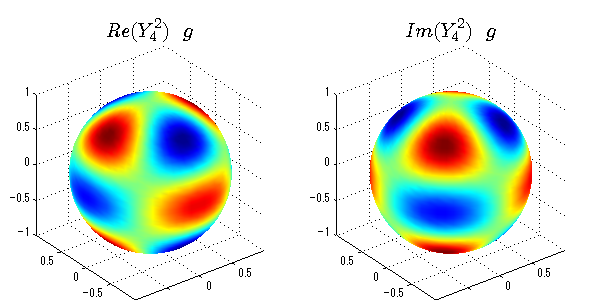
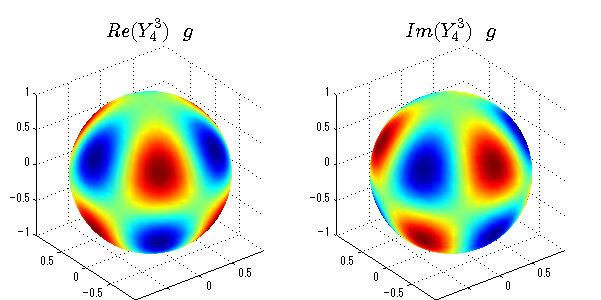
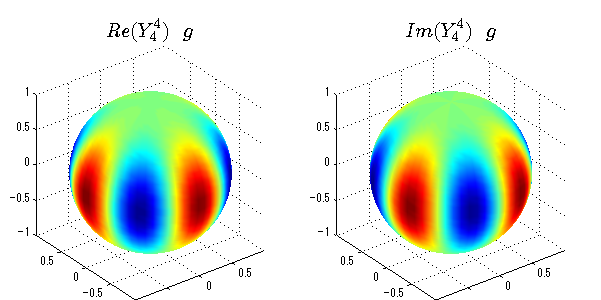
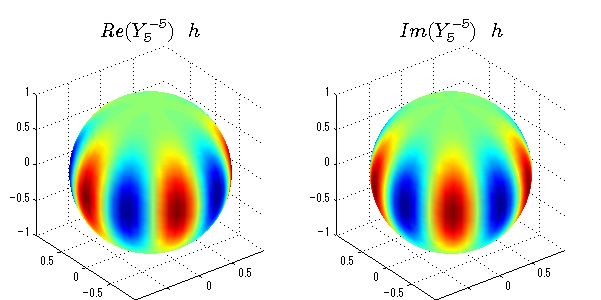
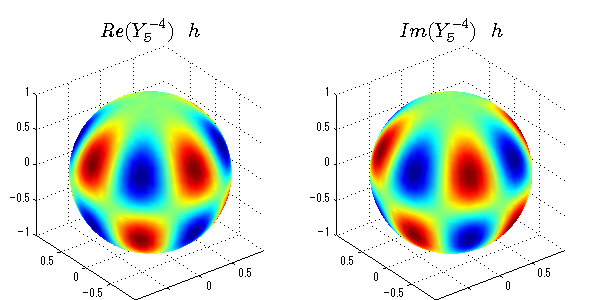
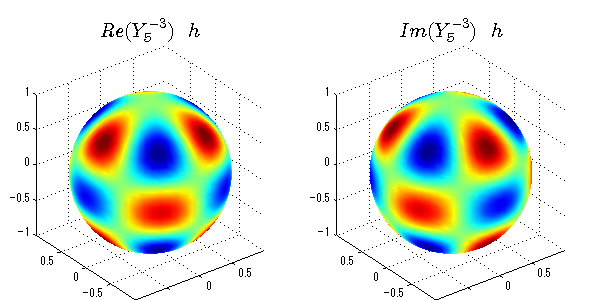
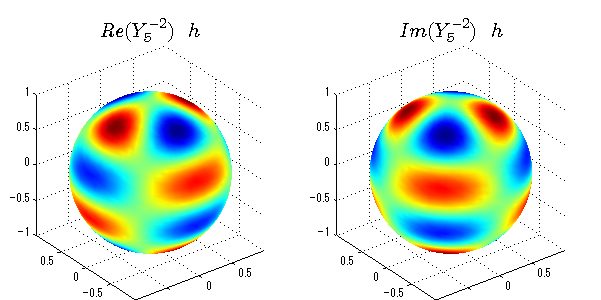
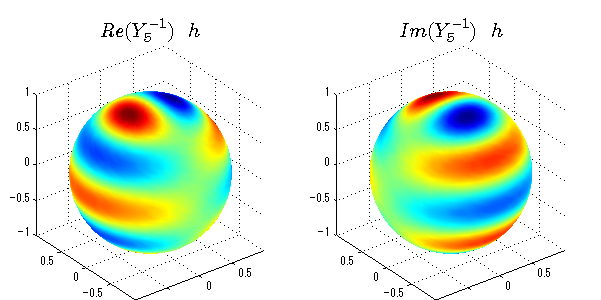
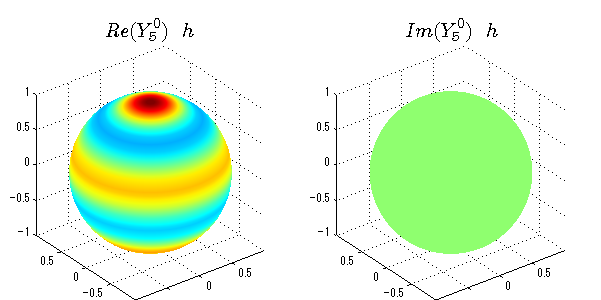
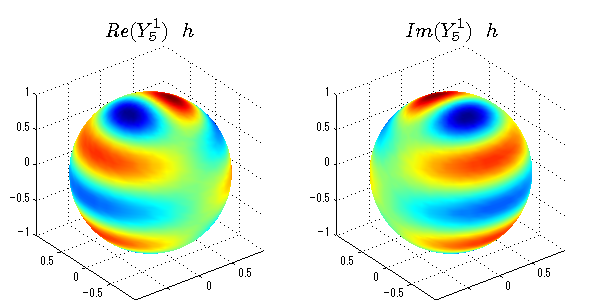
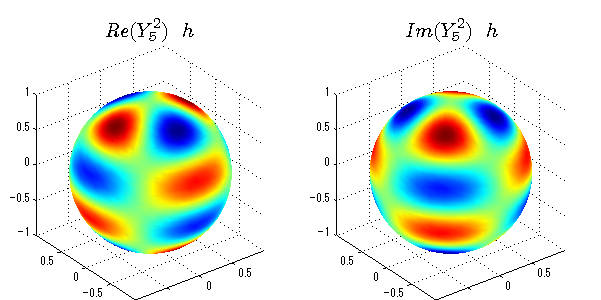
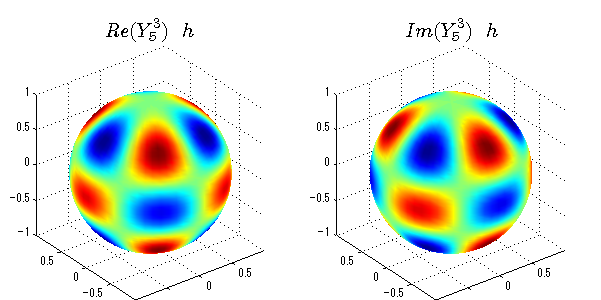
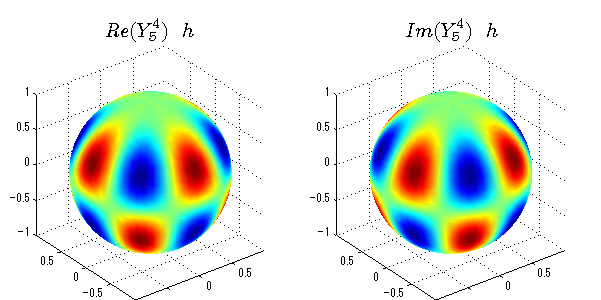
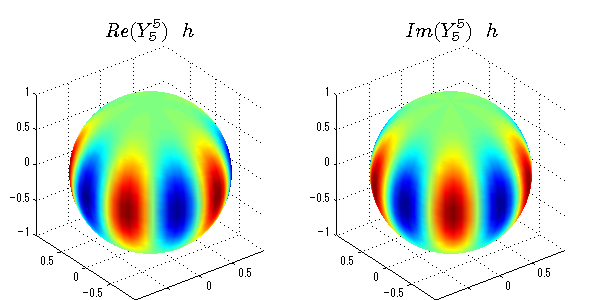
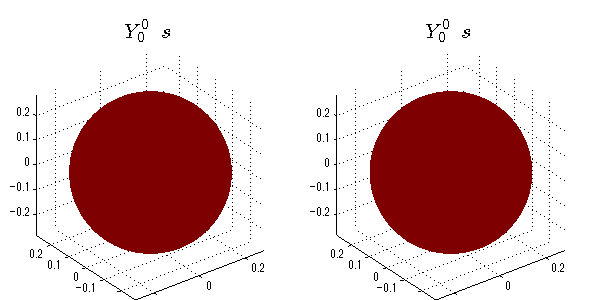
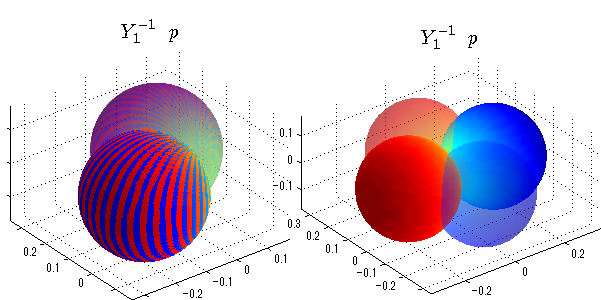
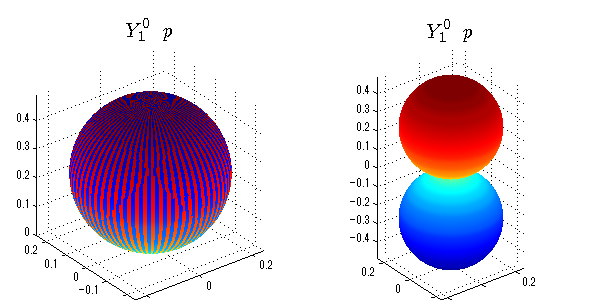
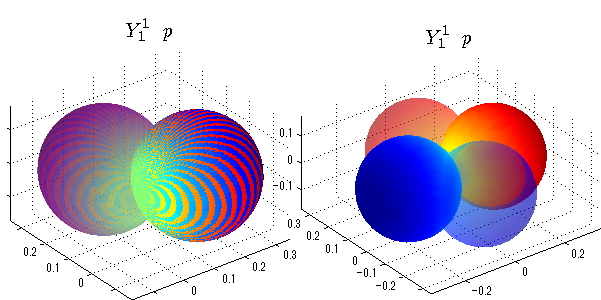
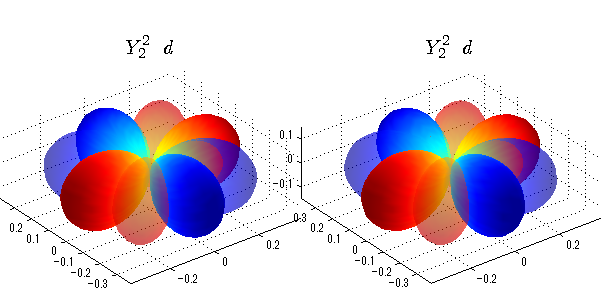
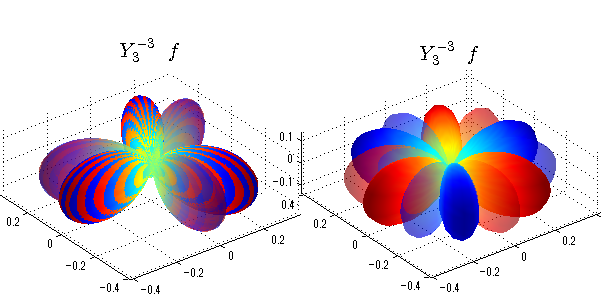
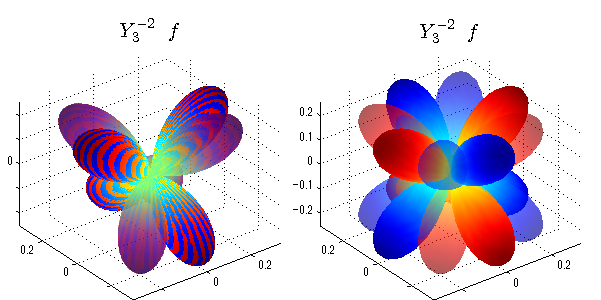
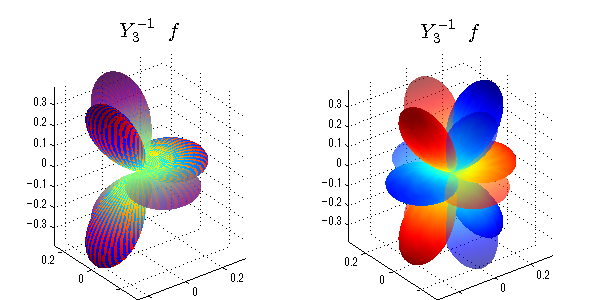
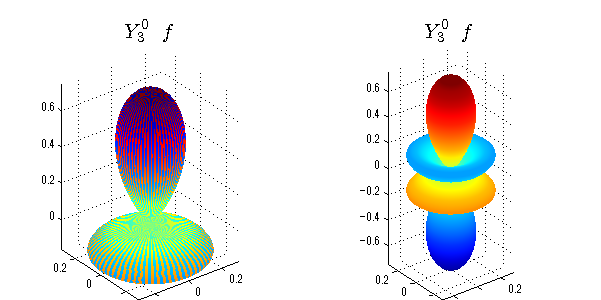
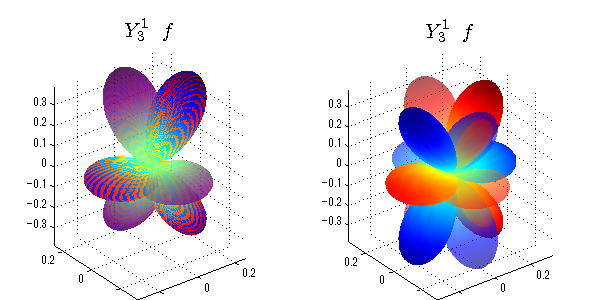
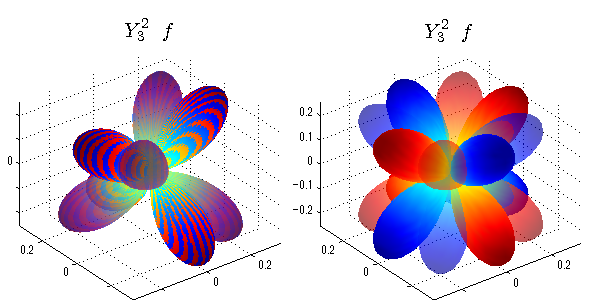
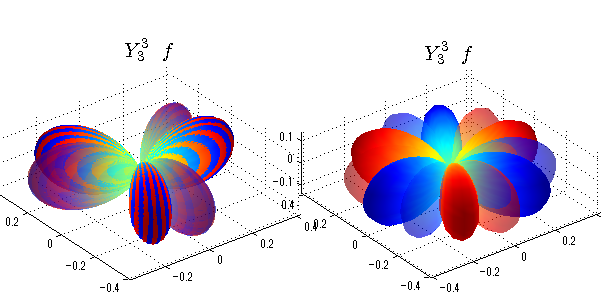
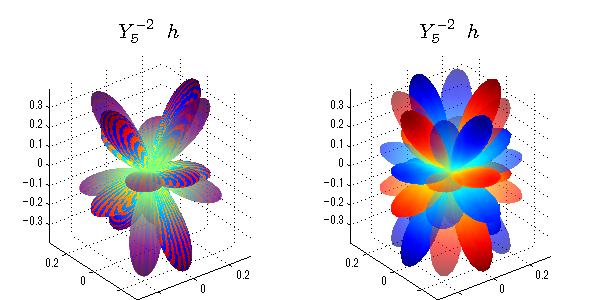
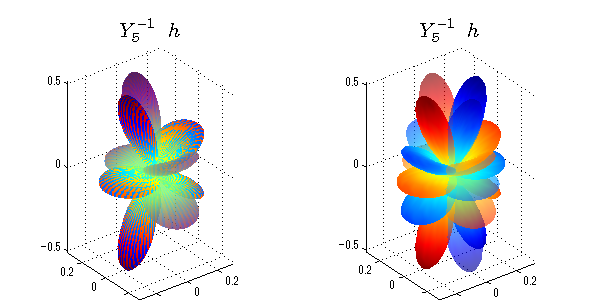
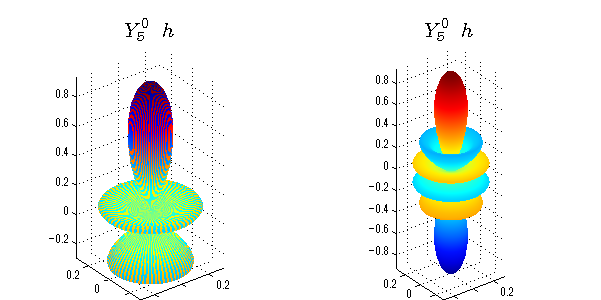
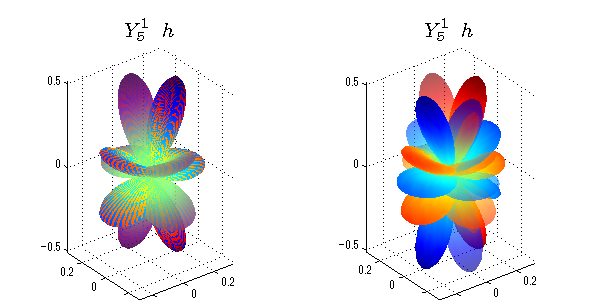
球面調和関数 半径の正負/絶対値表示
中心からの距離は実数・虚数の値を反映させました。 左図はマイナスの距離を含むそのままの値を、 右図はた時の絶対値で表しています。 色は実数・虚数部分の大きさを反映させました。 虚数部分は半透明にしてます。 中心からの距離を絶対値表示しないとlが奇数の時は、実数部分がマイナスの距離になり、表面が重なって縞々になります。
close all;clear; N=5; seg=64; theta=linspace(0,pi,seg); phi=linspace(0,2*pi,seg); Theta=theta'*ones(1,seg); Phi=ones(seg,1)*phi; x=sin(Theta).*cos(Phi); y=sin(Theta).*sin(Phi); z=cos(Theta); for l=0:N; L=legendre(l,cos(theta)); for m=-l:l; am=abs(m); LL=L(abs(m)+1,:); c=(-1)^((m+am)/2)*sqrt((2*l+1)/(4*pi)*factorial(l-am)/factorial(l+am))*LL'*exp(1i*m*phi); figure('color',[1,1,1],'inverthardcopy','off','position',[50,50,600,300]); for mm=1:2 subplot('position',[(mm-1)*0.5,0,0.5,0.85]); cc=real(c); if mm==1;r=cc;else r=abs(cc);end; h=surf(r.*x,r.*y,r.*z,cc);hold on; set(h,'FaceColor','interp','EdgeColor','none'); cc=imag(c); if mm==1;r=cc;else r=abs(cc);end; h=surf(r.*x,r.*y,r.*z,cc);hold on; set(h,'FaceColor','interp','EdgeColor','none','FaceAlpha',0.4); grid on; daspect([1,1,1]); axis tight; rotate3d on; st1=sprintf('Y_%d^{%d}',l,m); switch l case 0;st2='s'; case 1;st2='p'; case 2;st2='d'; case 3;st2='f'; case 4;st2='g'; case 5;st2='h'; end; title(['$$',st1,'\ \ ',st2,'$$'],'interpreter','latex','FontSize',15); end; end; end;
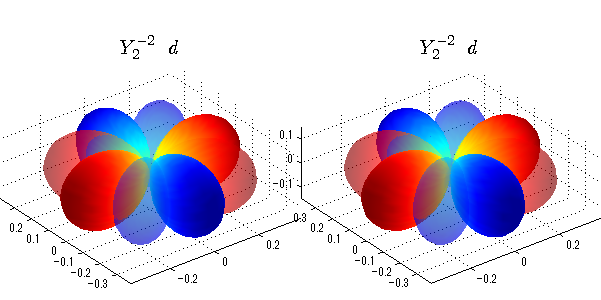
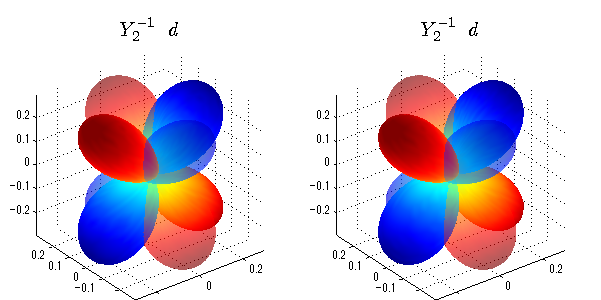
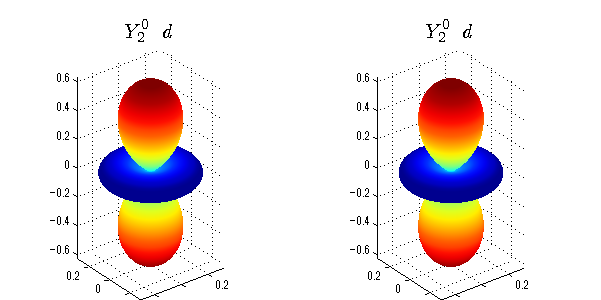
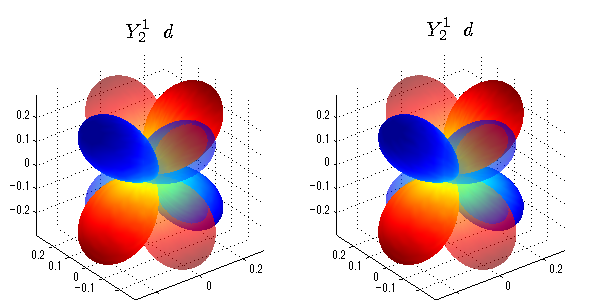
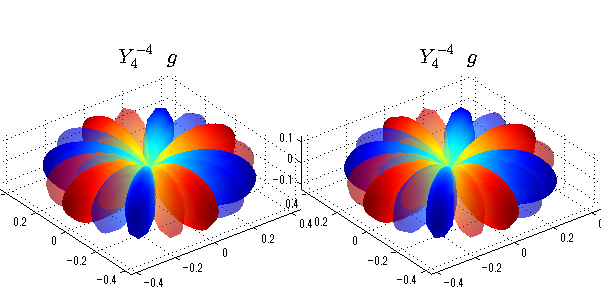
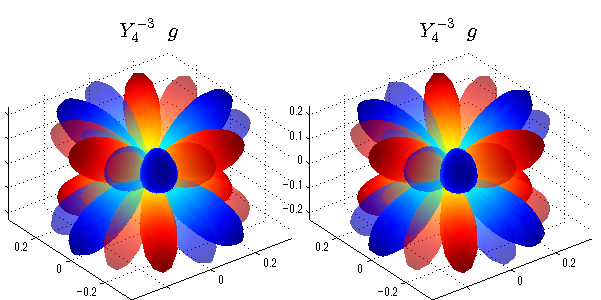
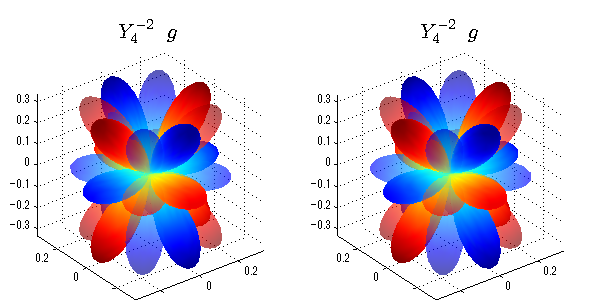
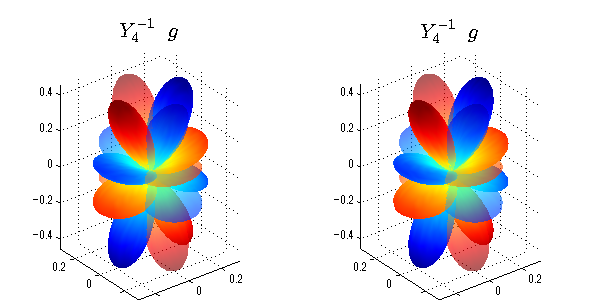
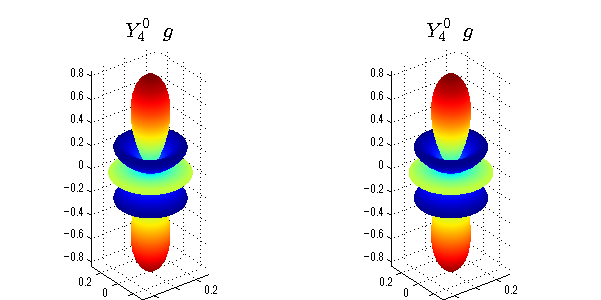
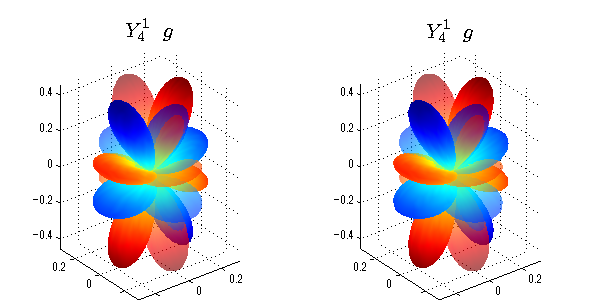
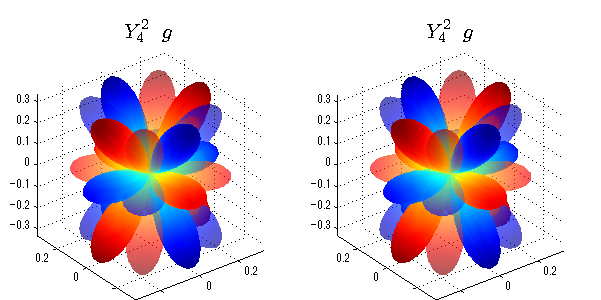
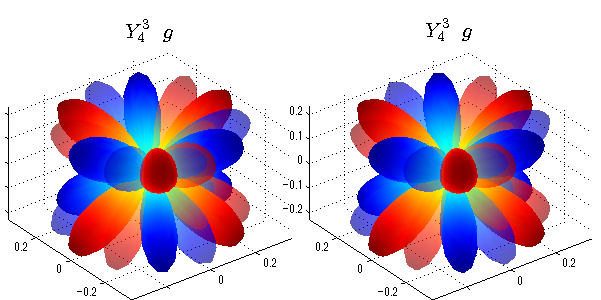
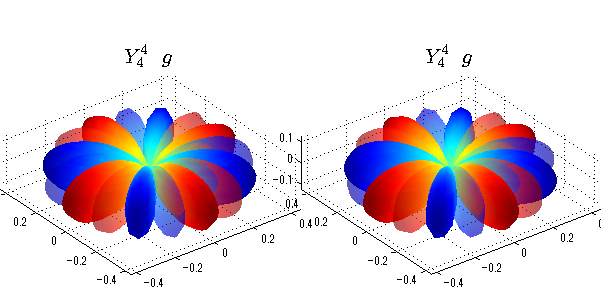
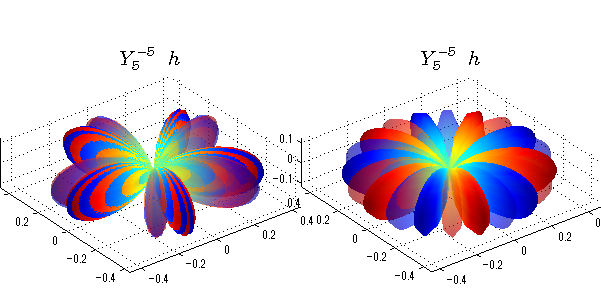
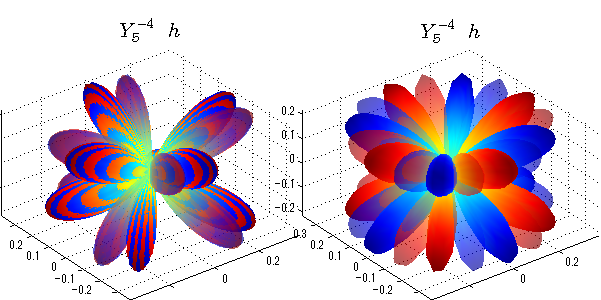
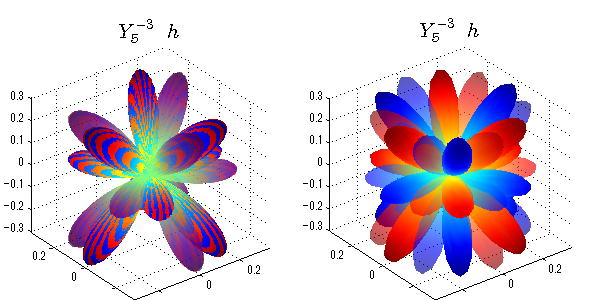
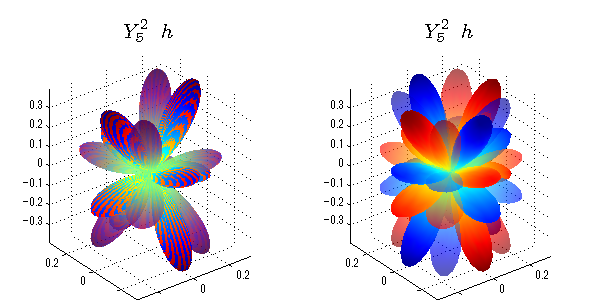
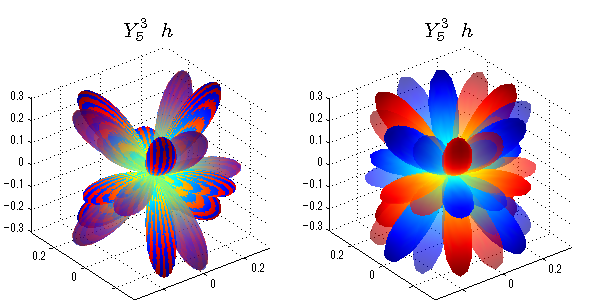
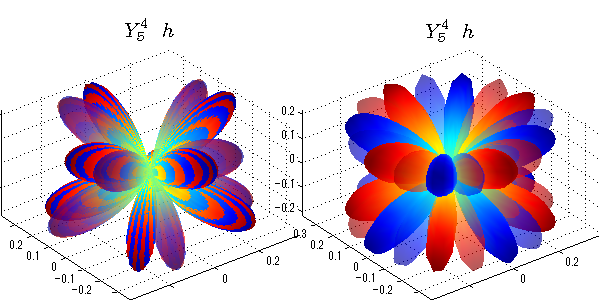
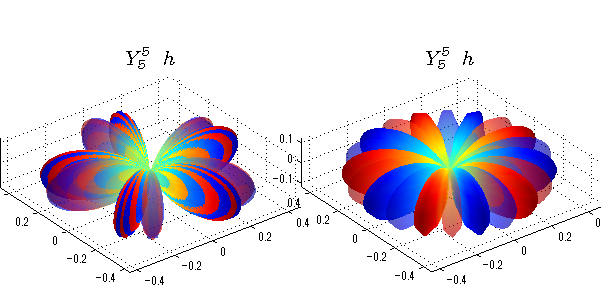
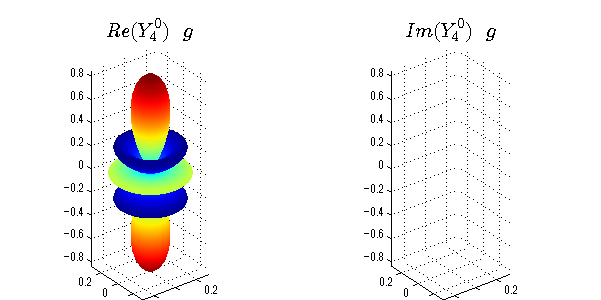
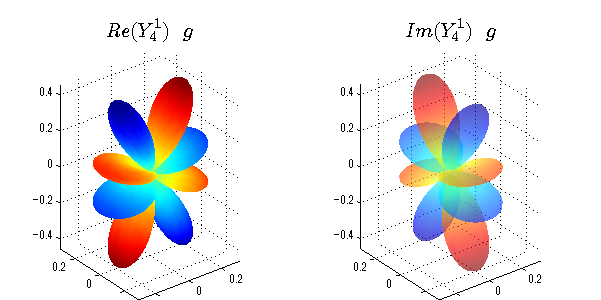
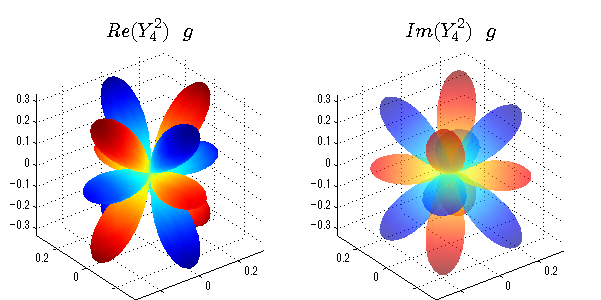
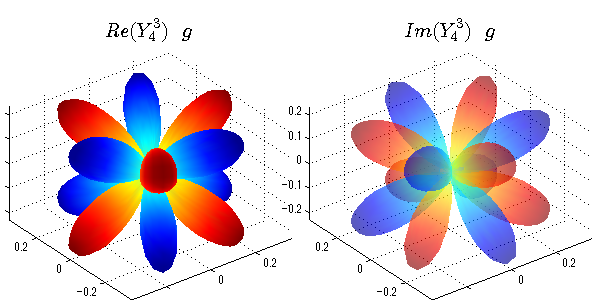
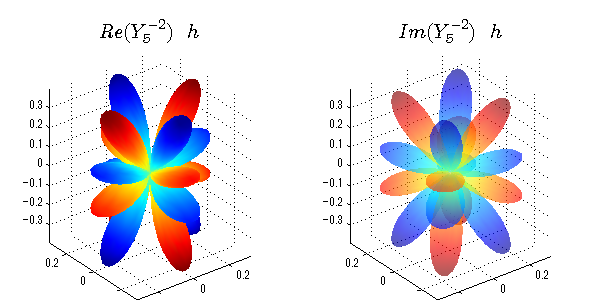
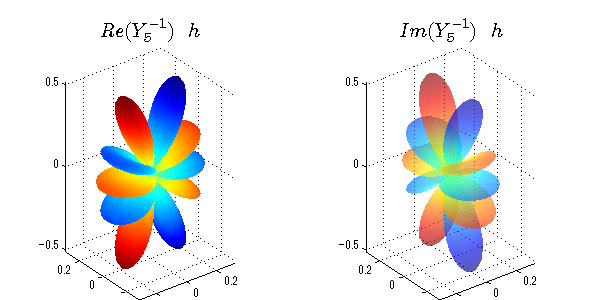
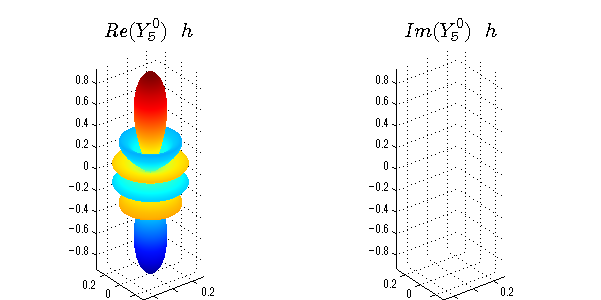
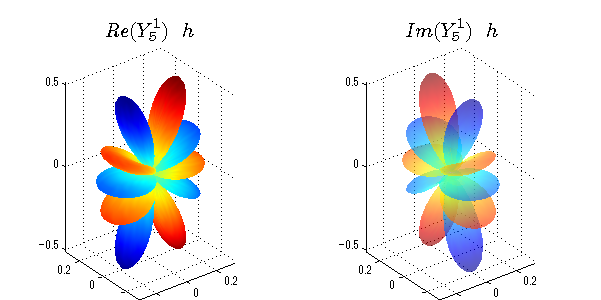
球面調和関数 実数・虚数別表示
実数と虚数に分けて表示させました。 左は実数部分、右は虚数部分です。虚数部分は半透明としました。 中心からの距離を実数・虚数の値の絶対値で反映させました。 色はマイナスが赤で、プラスが青です。
close all;clear; N=5; seg=64; theta=linspace(0,pi,seg); phi=linspace(0,2*pi,seg); Theta=theta'*ones(1,seg); Phi=ones(seg,1)*phi; x=sin(Theta).*cos(Phi); y=sin(Theta).*sin(Phi); z=cos(Theta); for l=0:N L=legendre(l,cos(theta)); for m=-l:l; am=abs(m); LL=L(abs(m)+1,:); c=(-1)^((m+am)/2)*sqrt((2*l+1)/(4*pi)*factorial(l-am)/factorial(l+am))*LL'*exp(1i*m*phi); figure('color',[1,1,1],'inverthardcopy','off','position',[50,50,600,300]); for mm=1:2 cc=abs(c); cx=cc.*x;cy=cc.*y;cz=cc.*z; cx=[min(cx(:)),max(cx(:))]; cy=[min(cy(:)),max(cy(:))]; cz=[min(cz(:)),max(cz(:))]; if mm==1; cc=real(c);r=abs(cc); else cc=imag(c);r=abs(cc); end; subplot('position',[(mm-1)*0.5,0,0.5,0.85]); h=surf(r.*x,r.*y,r.*z,cc);hold on; set(h,'FaceColor','interp','EdgeColor','none'); if mm==2;set(h,'FaceAlpha',0.4);end; grid on; daspect([1,1,1]); set(gca,'xlim',cx,'ylim',cy,'zlim',cz); % axis tight; rotate3d on; st1=sprintf('Y_%d^{%d}',l,m); if mm==1 st1=sprintf('Re(Y_%d^{%d})',l,m); else st1=sprintf('Im(Y_%d^{%d})',l,m); end; switch l case 0;st2='s';st3=''; case 1; st2='p'; switch m; case {-1,1};st3='_x';if mm==2;st3='_y';end; case 0;st3='_z'; if mm==2;st3=''; end; end; case 2; st2='d_{'; switch m; case {-2,2};st3='x^2-y^2}';if mm==2;st3='xy}';end; case {-1,1};st3='xz}'; if mm==2;st3='yz}';end; case 0;st3='3z^2-r^2}'; if mm==2;st3='}';end; end; case 3; st2='f_{'; switch m; case {-3,3};st3='x^3-3xy^2}'; if mm==2;st3='y^3-3xy^2}';end; case {-2,2};st3='x^2z-y^2z}'; if mm==2;st3='xyz}';end; case {-1,1};st3='xr^2-5xz^2}';if mm==2;st3='yr^2-5yz^2}';end; case 0;st3='5z^3-3zr^2}'; if mm==2;st3='}';end; end; case 4;st2='g';st3=''; case 5;st2='h';st3=''; end; title(['$$',st1,'\ \ ',st2,st3,'$$'],'interpreter','latex','FontSize',15); end; end; end;
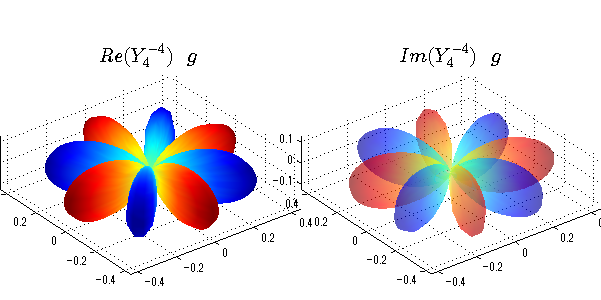
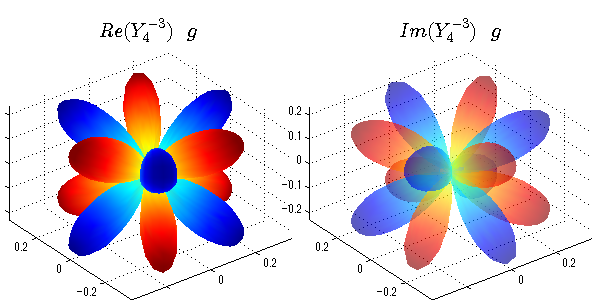
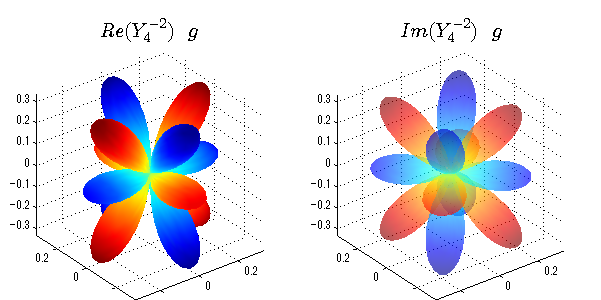
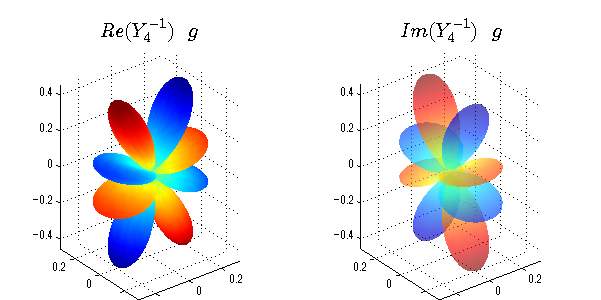
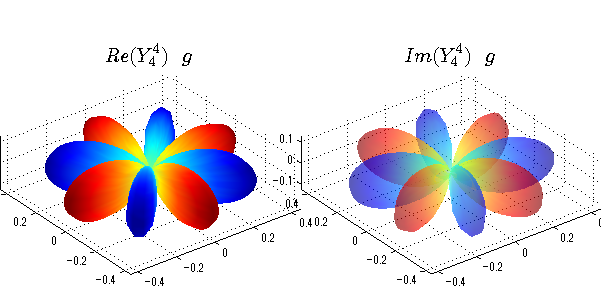
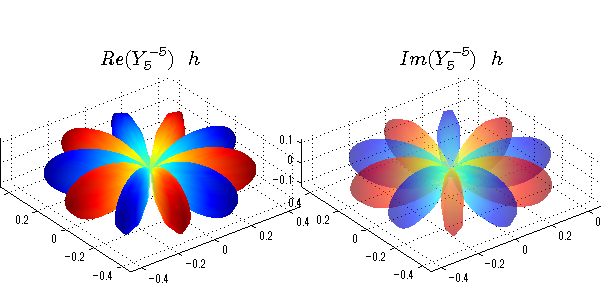
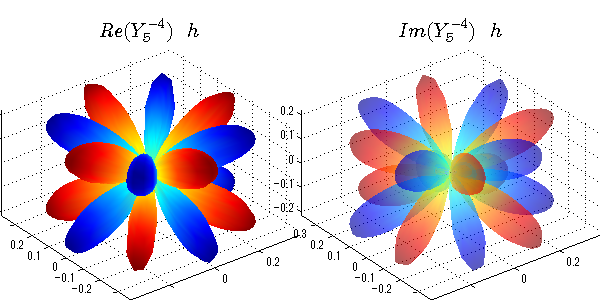
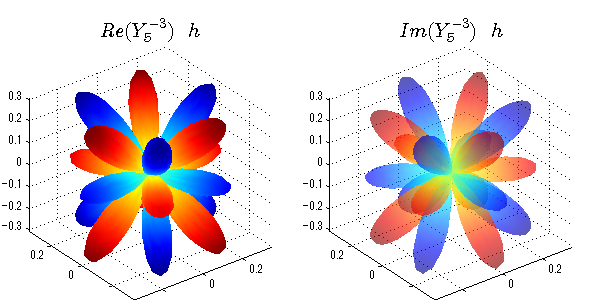
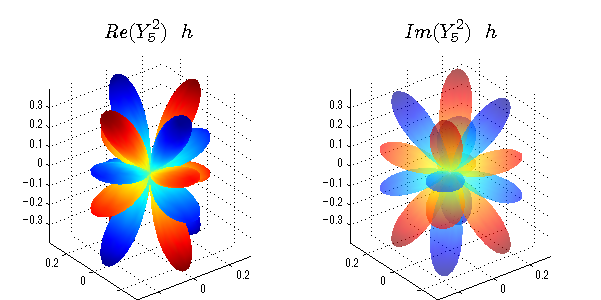
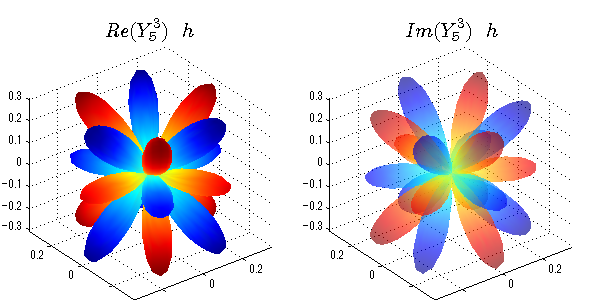
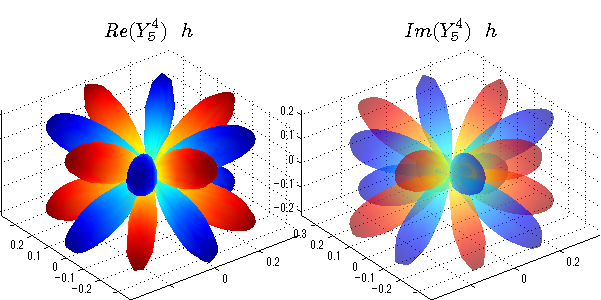
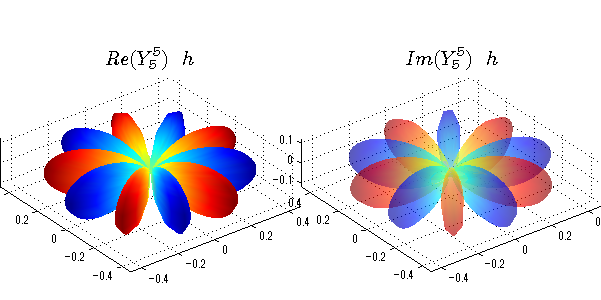
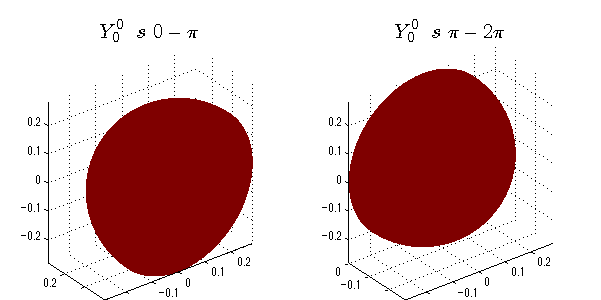
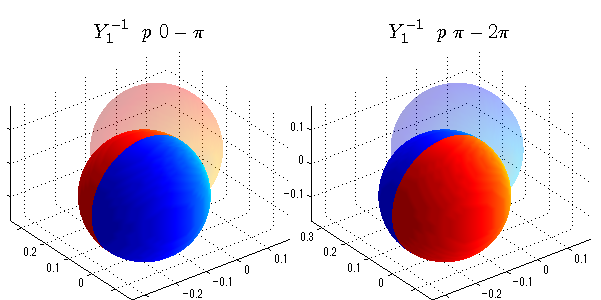
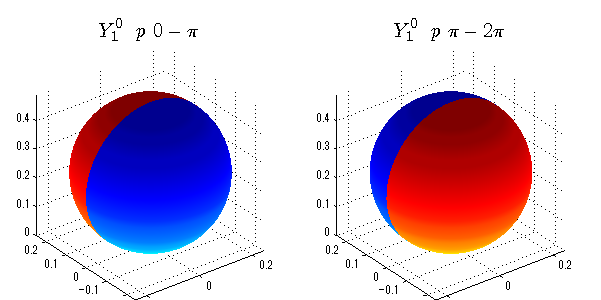
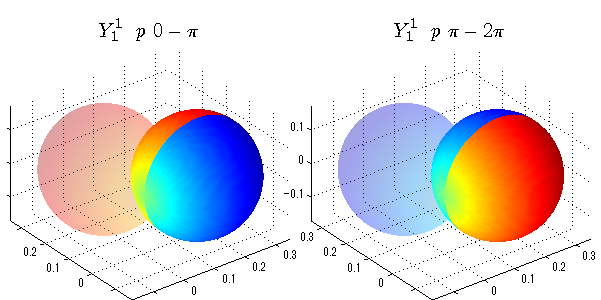
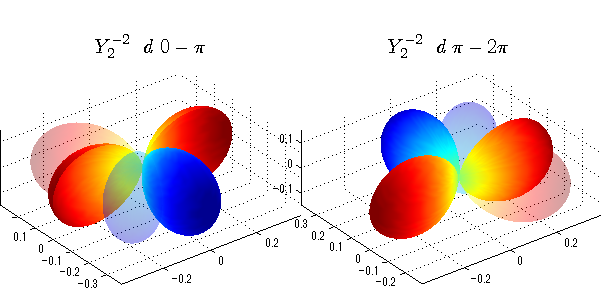
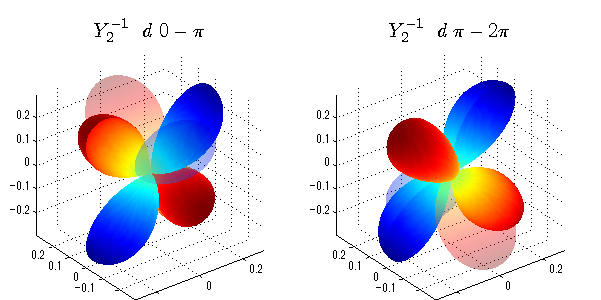
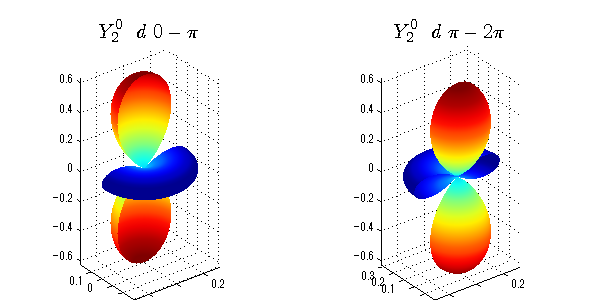
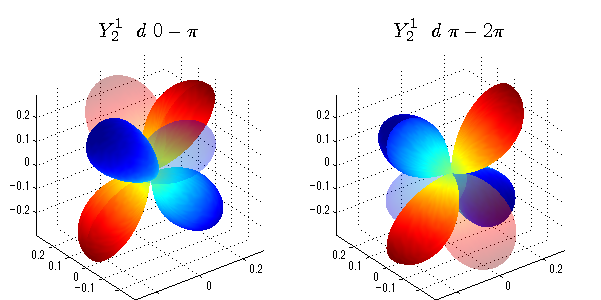
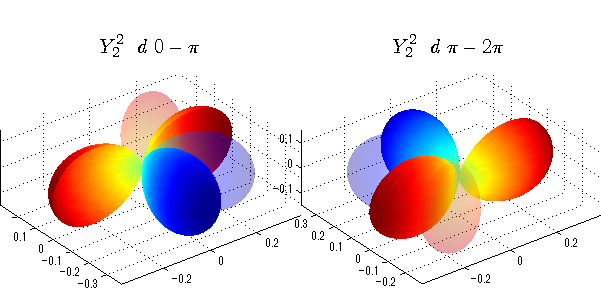
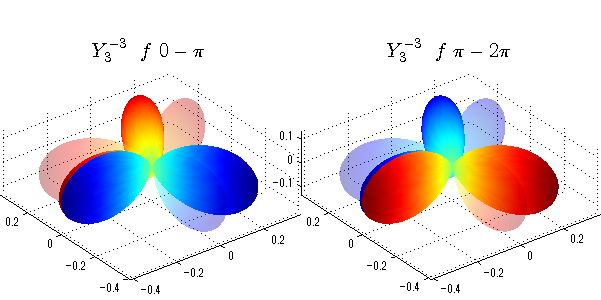
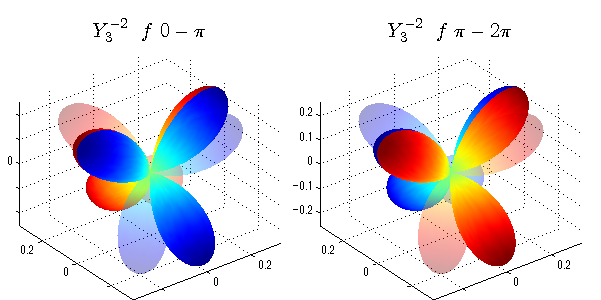
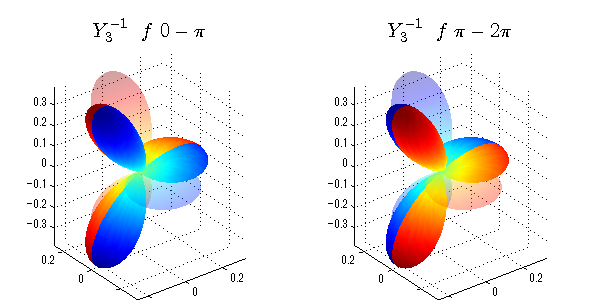
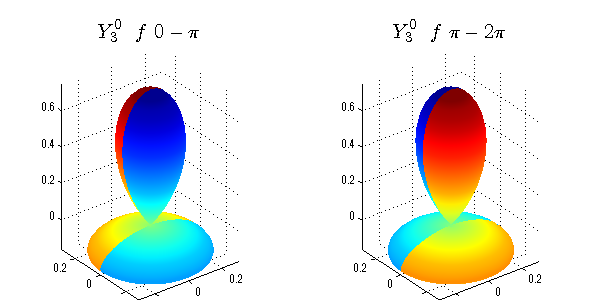
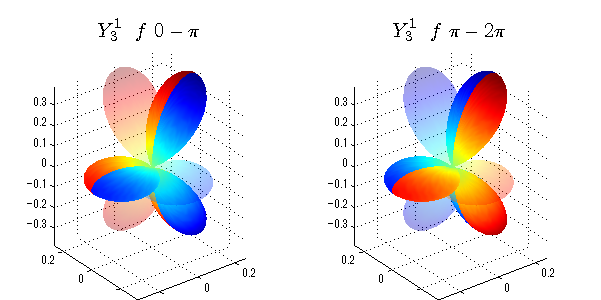
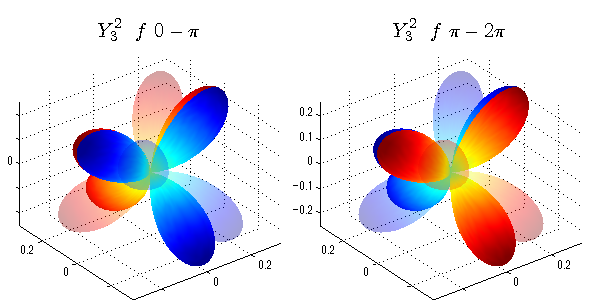
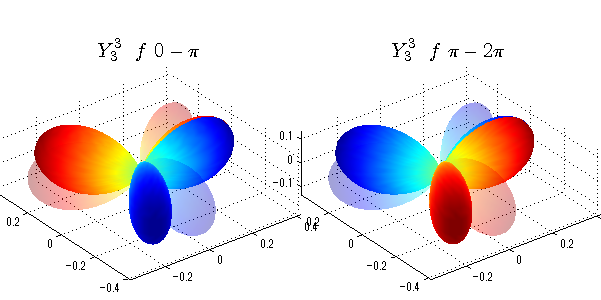
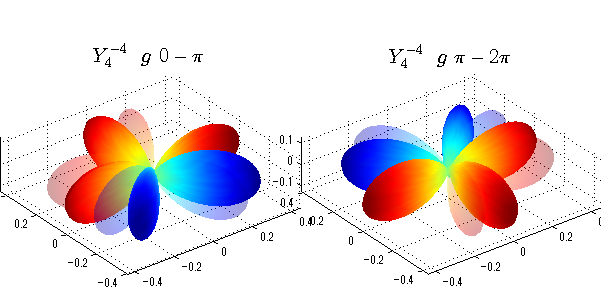
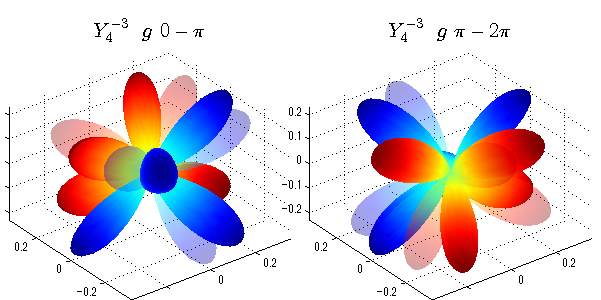
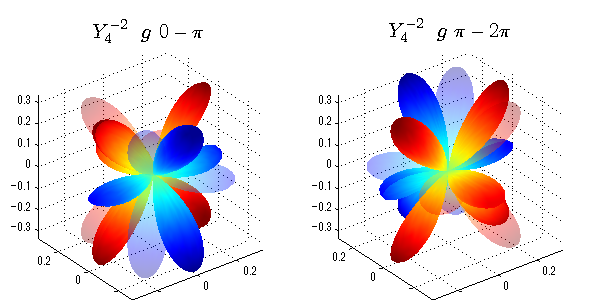
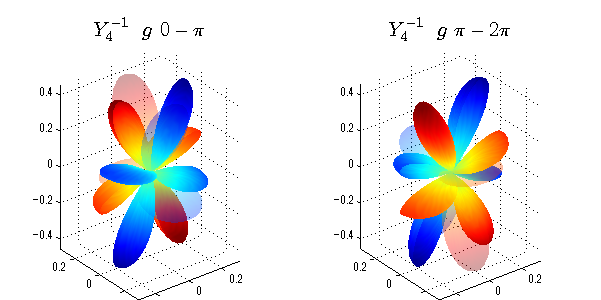
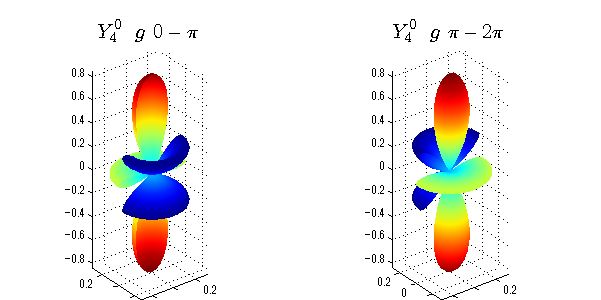
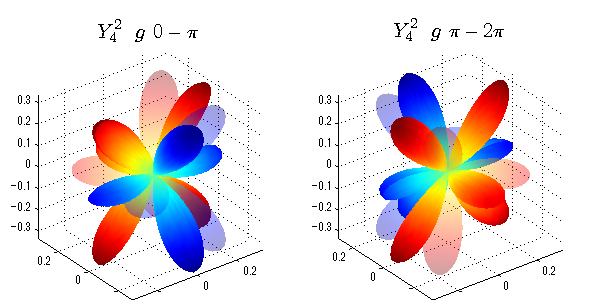
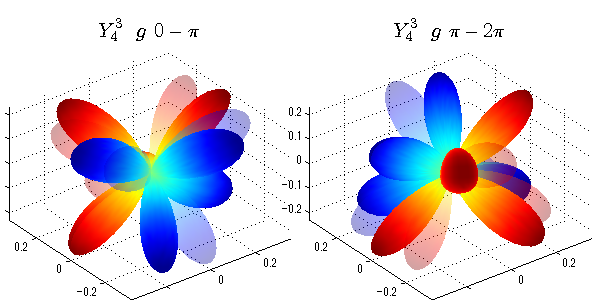
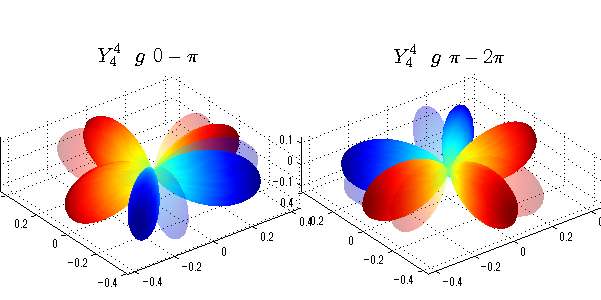
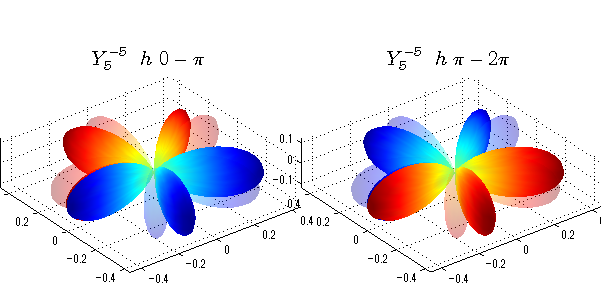
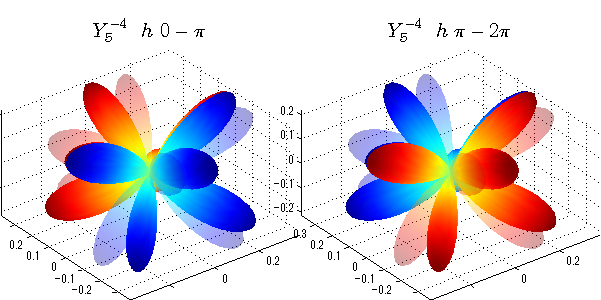
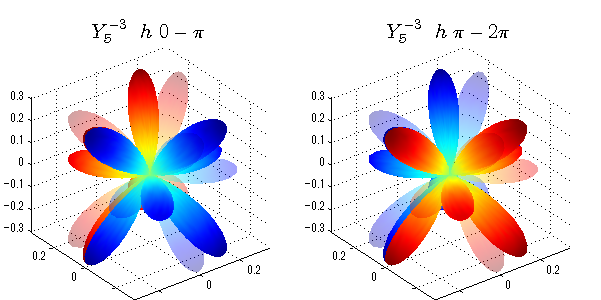
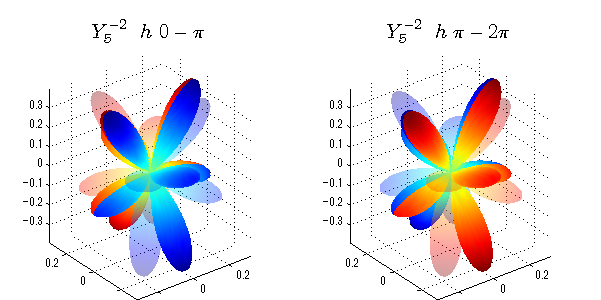
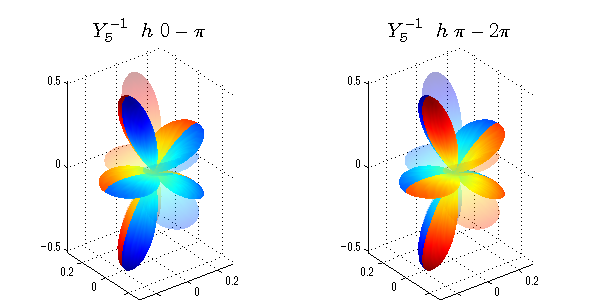
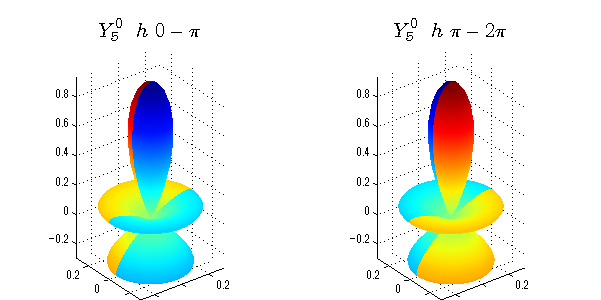
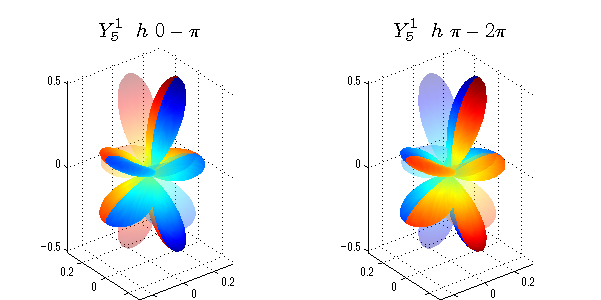
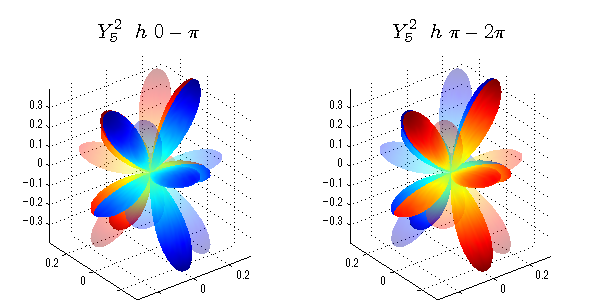
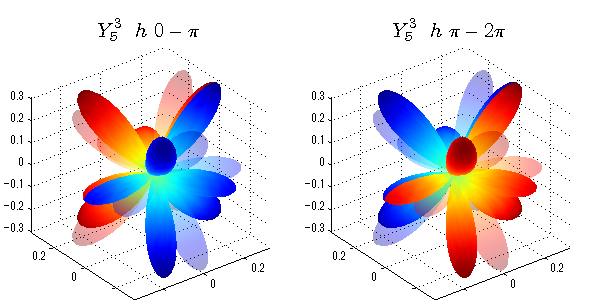
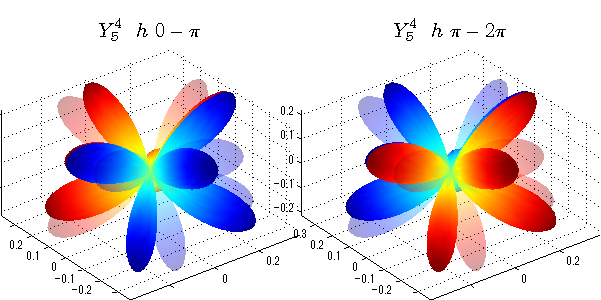
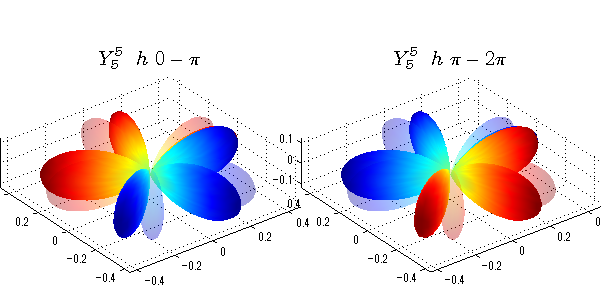
球面調和関数 位相別表示
phiを0~π、π~2πにわけて絶対値でなく、そのまま表示としました。
close all;clear; N=5; seg=64; theta=linspace(0,pi,seg); phi1=linspace(0,pi,seg); phi2=linspace(pi,2*pi,seg); Theta=theta'*ones(1,seg); Phi1=ones(seg,1)*phi1; Phi2=ones(seg,1)*phi2; x1=sin(Theta).*cos(Phi1); y1=sin(Theta).*sin(Phi1); x2=sin(Theta).*cos(Phi2); y2=sin(Theta).*sin(Phi2); z=cos(Theta); for l=0:N; L=legendre(l,cos(theta)); for m=-l:l; am=abs(m); LL=L(abs(m)+1,:); figure('color',[1,1,1],'inverthardcopy','off','position',[50,50,600,300]); for mm=1:2 switch mm case 1;phi=phi1;x=x1;y=y1; case 2;phi=phi2;x=x2;y=y2; end; c=(-1)^((m+am)/2)*sqrt((2*l+1)/(4*pi)*factorial(l-am)/factorial(l+am))*LL'*exp(1i*m*phi); subplot('position',[(mm-1)*0.5,0,0.5,0.85]); cc=real(c);r=cc; h=surf(r.*x,r.*y,r.*z,cc);hold on; set(h,'FaceColor','interp','EdgeColor','none'); cc=imag(c);r=cc; h=surf(r.*x,r.*y,r.*z,cc);hold on; set(h,'FaceColor','interp','EdgeColor','none','FaceAlpha',0.2); grid on; daspect([1,1,1]); axis tight; rotate3d on; st1=sprintf('Y_%d^{%d}',l,m); switch l case 0;st2='s'; case 1;st2='p'; case 2;st2='d'; case 3;st2='f'; case 4;st2='g'; case 5;st2='h'; end; if mm==1;st3='\ 0-\pi';else st3='\ \pi-2\pi';end; title(['$$',st1,'\ \ ',st2,st3,'$$'],'interpreter','latex','FontSize',15); end; end; end;